题目内容
【题目】如图，
内接于圆
，
为直径，点
在圆上，过点作圆的切线与
的延长线交于点
，点是弧
的中点，连结
交于点
．
（1）求证：
；
（2）若
，求的长．
【答案】（1）见详解；（2）
【解析】
（1）连接OD，根据圆周角定理的推论和等腰三角形的性质可知
，再根据切线的性质和等量代换可知
，再利用圆周角定理的推论可知
，从而有 
，最后利用同位角相等，两直线平行即可证明；
（2）连接BD，先根据勾股定理得出AF的长度，然后根据直角三角形两锐角互余和对顶角相等得出
，
，然后利用锐角三角函数得出
，进而求出AD的长度，最后再利用锐角三角函数即可求出AB的长度．
（1）连接OD，
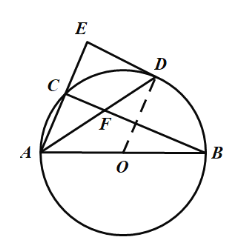
∵点
是弧
的中点，
∴
．
∵
，
∴
，
∴．
∵DE是圆
的切线，
∴
，
，
，
．
∵
为直径，
∴，
∴，
；
（2）连接BD，
∵
，
．
，
，
．
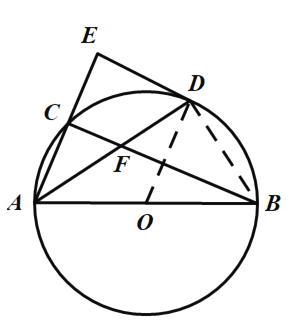
∵为直径，
∴
，
．
∵，
．
，
，
，
，
．
，
．
，
．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
