题目内容
2. 如图是“北大西洋公约组织”标志的主体部分(平面图),它是由四边形OABC绕点O进行3次旋转变换后形成的.测得AB=BC,OA=OC,∠ABC=40°,则∠OAB的度数是95°.
如图是“北大西洋公约组织”标志的主体部分(平面图),它是由四边形OABC绕点O进行3次旋转变换后形成的.测得AB=BC,OA=OC,∠ABC=40°,则∠OAB的度数是95°.
分析 先根据旋转的性质得到∠AOC=90°,再利用“SSS”可证明△ABO≌△CBO,则∠AOB=∠BOC=$\frac{1}{2}$∠AOC=45°,然后根据三角形内角和定理计算∠OAB的度数.
解答 解:∵“北大西洋公约组织”标志的主体部分(平面图)是由四边形OABC绕点O进行3次旋转变换后形成的,
∴∠AOC=$\frac{360°}{4}$=90°,
在△ABO和△CBO中
$\left\{\begin{array}{l}{AB=CB}\\{OA=OC}\\{OB=OB}\end{array}\right.$,
∴△ABO≌△CBO,
∴∠AOB=∠BOC,
即∠AOB=$\frac{1}{2}$∠AOC=45°,
在△AOB中,∠OAB=180°-45°-40°=95°.
故答案为95°.
点评 本题考查了全等三角形的判定与性质:全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.也考查了旋转的性质.

练习册系列答案
相关题目
18.将一质地均匀的正方体骰子掷一次,观察向上一面的点数,与点数4相差2的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
 如图,E是正方形ABCD内一点,EA=AB=BE.延长DE交BC于F,FG⊥BE于G.求证:EG=FG.
如图,E是正方形ABCD内一点,EA=AB=BE.延长DE交BC于F,FG⊥BE于G.求证:EG=FG.
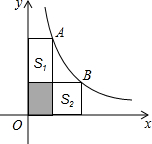 如图,A、B两点在双曲线$y=\frac{12}{x}$上,分别过A、B两点想坐标轴作垂线,若S阴影=3,则S1+S2的值为( )
如图,A、B两点在双曲线$y=\frac{12}{x}$上,分别过A、B两点想坐标轴作垂线,若S阴影=3,则S1+S2的值为( )
 如图,圆锥的轴截面是边长为9cm的正三角形ABC,P是母线AC的中点.求在圆锥的侧面上从B点到P点的最短路线的长.
如图,圆锥的轴截面是边长为9cm的正三角形ABC,P是母线AC的中点.求在圆锥的侧面上从B点到P点的最短路线的长. 已知抛物线y=-x2+2x+m.
已知抛物线y=-x2+2x+m.