Question

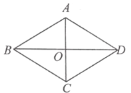
【题目】已知，如图，、、分别为数轴上的三个点，点对应的数为60，点在点的左侧，并且与点的距离为30，点在点左侧，点到距离是点到点距离的4倍．

（1）求出数轴上点对应的数及的距离．

（2）点从点出发，以3单位/秒的速度项终点运动，运动时间为秒．

①点点在之间运动时，则_______．（用含的代数式表示）

②点在点向点运动过程中，何时、、三点中其中一个点是另外两个点的中点？求出相应的时间．

③当点运动到点时，另一点以5单位/秒速度从点出发，也向点运动，点到达点后立即原速返回到点，那么点在往返过程中与点相遇几次？直接写出相遇是点在数轴上对应的数．

Answer 1

【答案】（1）点对应的数为30；AC=120；（2）①；②的值为5或20；③相遇2次；点在数轴上对应的数为－15或．

【解析】

(1)根据A点对应的数为60，B点在A点的左侧，AB=30求出B点对应的数，根据AC=4AB求出AC的距离；

(2)①当P点在AB之间运动时，根据路程=速度×时间求出AP=3t，根据BP=AB-AP求解；

②分P点是AB的中点和B点是AP的中点两种情况进行讨论即可；

③根据P、Q两点的运动速度与方向可知Q点在往返过程中与P点相遇2次，设Q点在往返过程中经过x秒与P点相遇，第一次相遇是点Q从A点出发，向C点运动的途中，根据AQ-BP=AB列出方程；第二次相遇是点Q到达C点后返回到A点的途中，根据CQ+BP=BC列出方程，进而求出P点在数轴上的对应的数．

解（1）点对应的数为60，,点在点的左侧，并且与点的距离为30，

点对应的数为；

点到点距离是,点到点距离的4倍，

;

（2）①当点在之间运动时，

，

．

故答案为；

②当点是、两点的中点时，，

，解得；

当点是两点的中点时，，

，解得．

故所求时间的值为5或20；

③相遇2次．

设点在往返过程中经过秒与点相遇．

第一次相遇是点从出发，向点运动的途中．

，

，

解得，

此时点在数轴上对应的数是：；

第二次相遇是到达点后返回到点的途中．

，

，

解得，

此时点在数轴上对应的数是：．

综上，相遇时点在数轴上对应的数为－15或．