题目内容
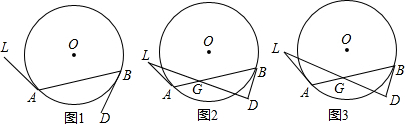
9.如图,AB为⊙O的弦,AL、BD都为⊙O的切线.(1)如图1,求证:∠LAB+∠ABD=180°;
(2)如图2,连接DL,且AL=BD,连接DL交AB于点G,求证:LG=DG;
(3)如图3,在(2)的条件下,若AG=3,⊙O的半径长为$\sqrt{19}$,∠BGD=30°,求DL的长.
分析 (1)由切线的性质得出.∠OAL=∠OBD=90°,再由∠OAB=∠OBA转化即可得出结论;
(2)先判断出∠LAB=∠DEA,AL=DE从而判断出△LAG≌△DEG即可得出结论;
(3)先判断出△OAL≌△OBD得出OL=OD,结合(2)得出的结论LG=DG,进而求出EF,FG,判断出OG⊥LD,然后构造出△OAG∽△DEF,即可求出DE,OG=$\sqrt{3}$FD,最后用勾股定理即可得出结论.
解答 解:(1)如图1,连接OA,OB, ∴OA=OB,
∴OA=OB,
∴∠OAB=∠OBA,
∵AL为⊙O的切线.
∴∠OAL=90°,
∵BD为⊙O的切线,
∴∠OBD=90°,
∴∠LAB+∠ABD=∠LAO+∠OAB+∠ABD=∠LAO+∠OBA+∠ABD=∠OAL+∠OBD=180°,
(2)如图2,在BG上取一点E,使DE=DB,
∴∠ABD=∠BED,
∵∠LAB+∠ABD=180°,
∴∠LAB+∠BED=180°,
∵∠BED+∠DEG=180°,
∴∠LAB=∠DEA,
∵AL=BD,
∴AL=DE,
在△LAG和△DEG中,$\left\{\begin{array}{l}{∠AGL=∠EGD}\\{∠LAG=DEA}\\{LA=DE}\end{array}\right.$,
∴△LAG≌△DEG,
∴LG=DG;
(3)如图4,连接OL,OA,OB,OG,OD,
在△OAL和△OBD中,$\left\{\begin{array}{l}{OA=OB}\\{∠OAL=∠OBD}\\{AL=BD}\end{array}\right.$,
∴△OAL≌△OBD,
∴OL=OD,
由(2)知,LG=DG,
∴∠OGL=∠OGD=90°,
∵∠AGL=∠BGD=30°,
∴∠AGO=120°,
过点E作EF⊥AB交DG于F,连接DE,如图3, 在Rt△GEF中,∠EGF=30°,EG=AG=3,
在Rt△GEF中,∠EGF=30°,EG=AG=3,
∴EF=$\sqrt{3}$,FG=2$\sqrt{3}$,
∴∠EFD=∠FEG+∠BGD=90°+30°=120°=∠AGO,
由(2)知,∠LAG=∠DEG,∠OAL=∠GEF,
∴∠OAG=∠DEF,
∴△OAG∽△DEF,
∴$\frac{OA}{DE}$=$\frac{AG}{EF}$=$\frac{OG}{DF}$,
设DF=x,
∵OA=$\sqrt{19}$,
∴$\frac{\sqrt{19}}{DE}=\frac{3}{\sqrt{3}}$=$\frac{OG}{x}$,
∴OG=$\sqrt{3}$x,DE=$\frac{\sqrt{57}}{3}$,
∴AL=DE=$\frac{\sqrt{57}}{3}$,
在Rt△OAL中,OL=$\sqrt{O{A}^{2}+A{L}^{2}}$=$\frac{2\sqrt{57}}{3}$,
在Rt△OGL中,OG2+LG2=OL2,
∴($\sqrt{3}$x)2+(2$\sqrt{3}$+$\sqrt{3}$x)2=($\frac{2\sqrt{57}}{3}$)2,
∴x=$\frac{-18+\sqrt{261}}{9}$(舍负取正),
∴LD=2LG=2DG=2(FG+DF)=2(2$\sqrt{3}$+$\frac{-18+\sqrt{261}}{9}$)=$\frac{36\sqrt{3}-36+2\sqrt{261}}{9}$.
点评 此题是圆的综合题,主要考查了圆的性质,全等三角形的性质和判定,勾股定理,相似三角形的性质和判定,解本题的关键是判断出LG=DG,作出辅助线是解本题的难点.

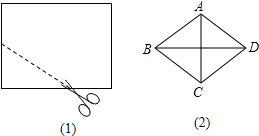 如图,将一个长为10cm,宽为8cm的矩形纸片先按照从左向右对折,再按照从下向上的方向对折,沿所得矩形两邻边中点的连线(虚线)剪下(如图(1)),再打开,得到如图(2)所示的小菱形的面积为( )
如图,将一个长为10cm,宽为8cm的矩形纸片先按照从左向右对折,再按照从下向上的方向对折,沿所得矩形两邻边中点的连线(虚线)剪下(如图(1)),再打开,得到如图(2)所示的小菱形的面积为( )| A. | 10cm2 | B. | 20cm2 | C. | 40cm2 | D. | 80cm2 |
| A. | +(-2)和-(+2) | B. | -|-3|和+(-3) | C. | (-1)2和-12 | D. | (-1)3和-13 |
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | 以上答案均不对 |
| A. | -2<a<-1 | B. | -2≤a<-1 | C. | -2<a≤-1 | D. | -2≤a≤-1 |
| A. | 2013 | B. | 2014 | C. | -1 | D. | 1 |
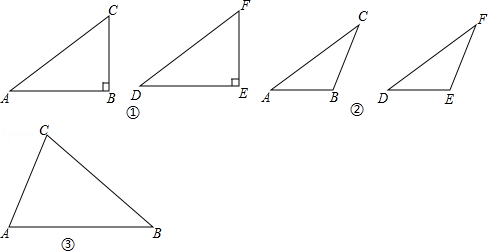
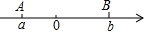 数学实验室:
数学实验室: