题目内容

20．公园有一块正方形的空地，后来从这块空地上划出部分区域栽种鲜花（如图），原空地一边减少了1m，另一边减少了2m，剩余空地的面积为18m2，求原正方形空地的边长．设原正方形的空地的边长为xm，则可列方程为（　　）
A．（x+1）（x+2）=18B．x2-3x+16=0C．（x-1）（x-2）=18D．x2+3x+16=0

分析 可设原正方形的边长为xm，则剩余的空地长为（x-1）m，宽为（x-2）m．根据长方形的面积公式方程可列出．

解答 解：设原正方形的边长为xm，依题意有
（x-1）（x-2）=18，
故选C．

点评 本题考查了由实际问题抽象出一元二次方程的知识，应熟记长方形的面积公式．另外求得剩余的空地的长和宽是解决本题的关键．

练习册系列答案
相关题目
10．在下面四个几何体中，主视图与俯视图都是圆的为（　　）
A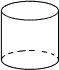．B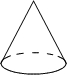．C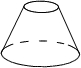．D．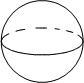
11．解方程：6（x-2）=8x+3．
8．我省某苹果基地销售优质苹果，该基地对需要送货且购买量在2000kg-5000kg（含2000kg和5000kg）的客户有两种销售方案（客户只能选择其中一种方案）：
方案A：每千克5.8元，由基地免费送货．
方案B：每千克5元，客户需支付运费2000元．
（1）请分别写出按方案A，方案B购买这种苹果的应付款y（元）与购买量x（kg）之间的函数表达式；
（2）求购买量x在什么范围时，选用方案A比方案B付款少；
（3）某水果批发商计划用20000元，选用这两种方案中的一种，购买尽可能多的这种苹果，请直接写出他应选择哪种方案．
15．如图，菱形ABCD的边AB=8，∠B=60°，P是AB上一点，BP=3，Q是CD边上一动点，将梯形APQD沿直线PQ折叠，A的对应点A′．当CA′的长度最小时，CQ的长为（　　）
A．5B．7C．8D．$\frac{13}{2}$
5．已知M、N、P、Q四点的位置如图所示，下列结论中，正确的是（　　）
A．∠NOQ=42°B．∠NOP=132°C．∠PON比∠MOQ大D．∠MOQ与∠MOP互补
12．随州市尚市“桃花节”观赏人数逐年增加，据有关部门统计，2014年约为20万人次，2016年约为28.8万人次，设观赏人数年均增长率为x，则下列方程中正确的是（　　）
A．20（1+2x）=28.8B．28.8（1+x）2=20
C．20（1+x）2=28.8D．20+20（1+x）+20（1+x）2=28.8
9．林业部门要考察某种幼树在一定条件下的移植成活率，下表是这种幼树在移植过程中的一组数据：
移植的棵数n10001500250040008000150002000030000
成活的棵数m8651356222035007056131701758026430
成活的频率$\frac{m}{n}$0.8650.9040.8880.8750.8820.8780.8790.881
估计该种幼树在此条件下移植成活的概率为0.881．
10．如图，CD是⊙O的直径，已知∠1=30°，则∠2=（　　）
A．30°B．45°C．60°D．70°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网