题目内容
15.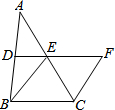 如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到F,使得EF=BE,连接CF.
如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到F,使得EF=BE,连接CF.(1)求证:四边形BCFE是菱形.
(2)若DE=4cm,∠EBC=60°,求菱形BCFE的面积.
分析 (1)先判断DE为△ABC的中位线得到DE∥BC且2DE=BC,加上BE=2DE,EF=BE,则EF=BC,EF∥BC,所以可判断四边形BCFE是平行四边形,然后再判断四边形BCFE是菱形;
(2)先计算出BC=2DE=8,再判断△BCE为等边三角形,根据等边三角形的面积公式得到S△BCE=16$\sqrt{3}$,所以菱形BCFE的面积=2S△BCE=32$\sqrt{3}$(cm2).
解答 (1)证明:∵D、E分别是AB、AC的中点,
∴DE为△ABC的中位线,
∴DE∥BC且2DE=BC,
又∵BE=2DE,EF=BE,
∴EF=BC,EF∥BC,
∴四边形BCFE是平行四边形,
又∵BE=FE,
∴四边形BCFE是菱形;
(2)解:∵DE=4,
∴BC=2DE=8,
∵∠EBC=60°,
而BE=BC,
∴△BCE为等边三角形,
∴S△BCE=$\frac{\sqrt{3}}{4}$×82=16$\sqrt{3}$,
∴菱形BCFE的面积=2S△BCE=32$\sqrt{3}$(cm2).
点评 本题考查了菱形的判定与性质:菱形是在平行四边形的前提下定义的,首先它是平行四边形,但它是特殊的平行四边形,特殊之处就是“有一组邻边相等”,因而就增加了一些特殊的性质和不同于平行四边形的判定方法.也考查了等边三角形的判定与性质.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
20.下列图形中,既是中心对称图形又是轴对称图形的是( )
| A. | 等边三角形 | B. | 矩形 | C. | 等腰梯形 | D. | 平行四边形 |
7.直角三角形一条直角边和斜边的长分别是一元二次方程x2-9x+20=0的两个实数根,则该三角形的面积是( )
| A. | 6 | B. | 6或10 | C. | 10 | D. | 12 |
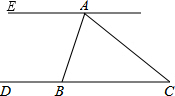 如图,在△ABC中,∠C=40°,CA=CB,过A点作EA∥BC,则∠EAB=70°.
如图,在△ABC中,∠C=40°,CA=CB,过A点作EA∥BC,则∠EAB=70°.
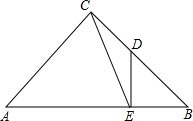 如图,△ABC是等腰三角形,∠ACB=90°,过BC的中点D作DE⊥AB,垂足为E,连接CE,求tan∠ACE的值.
如图,△ABC是等腰三角形,∠ACB=90°,过BC的中点D作DE⊥AB,垂足为E,连接CE,求tan∠ACE的值.