题目内容
17.抛物线y=ax2+bx+c的对称轴是x=-$\frac{b}{2a}$,顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$).(1)当a>0时,抛物线开口向上,当x>-$\frac{b}{2a}$时,y随x的增大而增大;当x<-$\frac{b}{2a}$时,y随x的增大而减小;当x=-$\frac{b}{2a}$时,y取最小值,为$\frac{4ac-{b}^{2}}{4a}$.
(2)当a<0时,抛物线开口向下,当x>-$\frac{b}{2a}$时,y随x的增大而减小;当x<-$\frac{b}{2a}$时,y随x的增大而增大;当x=-$\frac{b}{2a}$时,y取最大值,为$\frac{4ac-{b}^{2}}{4a}$.
分析 依据二次函数的对称轴方程和顶点坐标公式以及二次函数的图象和性质回答即可.
解答 解:物线y=ax2+bx+c的对称轴是x=-$\frac{b}{2a}$,顶点坐标是(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$).
(1)当a>0时,抛物线开口向上,当x>-$\frac{b}{2a}$时,y随x的增大而增大;当x<-$\frac{b}{2a}$时,y随x的增大而减小;当x=-$\frac{b}{2a}$时,y取最小值,为$\frac{4ac-{b}^{2}}{4a}$.
(2)当a<0时,抛物线开口向下,当x>-$\frac{b}{2a}$时,y随x的增大而减小;当x<-$\frac{b}{2a}$时,y随x的增大而增大;当x=-$\frac{b}{2a}$时,y取最大值,为$\frac{4ac-{b}^{2}}{4a}$.
故答案为:x=-$\frac{b}{2a}$;(-$\frac{b}{2a}$,$\frac{4ac-{b}^{2}}{4a}$);(1)向上;增大;减小;小;$\frac{4ac-{b}^{2}}{4a}$;(2)向下;减小;增大;大;$\frac{4ac-{b}^{2}}{4a}$.
点评 本题主要考查的是二次函数的性质,掌握二次函数的性质是解题的关键.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
5.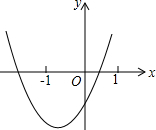 二次函数y=ax2+bx+c的图象如图所示,则下列关于a、b、c间的关系判断正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列关于a、b、c间的关系判断正确的是( )
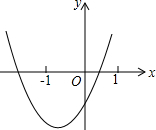 二次函数y=ax2+bx+c的图象如图所示,则下列关于a、b、c间的关系判断正确的是( )
二次函数y=ax2+bx+c的图象如图所示,则下列关于a、b、c间的关系判断正确的是( )| A. | ab<0 | B. | bc>0 | C. | a+b+c>0 | D. | a-b+c>0 |
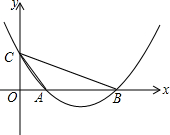 如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于C点且A(1,0),C(0,2)
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于C点且A(1,0),C(0,2) 如图,∠DAB+∠CDA=180°,∠ABC=∠EAD,直线AB与CD平行吗?直线AD与直线BC呢?为什么?
如图,∠DAB+∠CDA=180°,∠ABC=∠EAD,直线AB与CD平行吗?直线AD与直线BC呢?为什么?