题目内容
 如图所示,在平面直角坐标系中,已知A(6,
如图所示,在平面直角坐标系中,已知A(6,| 9 |
| 2 |
(1)以原点O为位似中心,将AB按相似比2:1放大,并且对应线段CD在y轴左侧,其中,点C与点A对应,点D与点B对应,直接写出C、D两点的坐标;
(2)在(1)中,若将y轴正半轴上的点P作为位似中心,其余条件不变,且点A的对应点C恰好在x轴上,求OP的长;
(3)试探究(2)中的
| 1 |
| AB |
| 1 |
| CD |
| 1 |
| OP |
考点:相似形综合题
专题:
分析:(1)根据位似图形的定义及其性质,直接写出C、D两点的坐标即可解决问题.
(2)如图,作出图形;利用相似三角形的性质,列出比例式即可解决问题.
(3)通过△OBP∽△CBD,得到
=
①;通过△POC∽△ABC,得到
=
②,由①+②即可解决问题.
(2)如图,作出图形;利用相似三角形的性质,列出比例式即可解决问题.
(3)通过△OBP∽△CBD,得到
| OP |
| CD |
| OB |
| BC |
| OP |
| AB |
| OC |
| BC |
解答: 解:(1)点C、点D的坐标分别为C(-12,-9)、D(-12,0).
解:(1)点C、点D的坐标分别为C(-12,-9)、D(-12,0).
(2)如图,连接AC、BD,则必过点P;
由位似图形的性质知:△BAP∽△CDP,
∴
=
,而DC=2AB,
∴CP=2AP,设AP=λ,则CP=2λ,AC=3λ;
∵OP∥AB,
∴△POC∽△ABC,
∴
=
=
,而AB=
,
∴OP=
×
=3.
(3)由题意知:CD∥AB,而OP∥AB,
∴CD∥OP,△OBP∽△CBD,
∴
=
①;
∵△POC∽△ABC,
∴
=
②,由①+②得:
+
=
,
而OB+OC=BC,
∴
+
=1,两端除以OP得:
+
=
.
 解:(1)点C、点D的坐标分别为C(-12,-9)、D(-12,0).
解:(1)点C、点D的坐标分别为C(-12,-9)、D(-12,0).(2)如图,连接AC、BD,则必过点P;
由位似图形的性质知:△BAP∽△CDP,
∴
| AP |
| CP |
| AB |
| CD |
∴CP=2AP,设AP=λ,则CP=2λ,AC=3λ;
∵OP∥AB,
∴△POC∽△ABC,
∴
| OP |
| AB |
| PC |
| AC |
| 2λ |
| 3λ |
| 9 |
| 2 |
∴OP=
| 2 |
| 3 |
| 9 |
| 2 |
(3)由题意知:CD∥AB,而OP∥AB,
∴CD∥OP,△OBP∽△CBD,
∴
| OP |
| CD |
| OB |
| BC |
∵△POC∽△ABC,
∴
| OP |
| AB |
| OC |
| BC |
| OP |
| CD |
| OP |
| AB |
| OB+OC |
| BC |
而OB+OC=BC,
∴
| OP |
| CD |
| OP |
| AB |
| 1 |
| AB |
| 1 |
| CD |
| 1 |
| OP |
点评:该题以平面直角坐标系为载体,以位似变换为方法,以相似三角形的判定及其性质的应用为考查的核心构造而成;解题的关键是深入观察、大胆猜测、合理推断、科学论证.

练习册系列答案
相关题目
若方程(a-2)x|a|-3x=1是关于x的一元二次方程,则a是( )
| A、2 | B、-2 | C、±2 | D、±1 |
 如图,点A、B、O是正方形网格上的三个格点,⊙O的半径为OA,点P是优弧
如图,点A、B、O是正方形网格上的三个格点,⊙O的半径为OA,点P是优弧 |
| AMB |
| A、30° | B、45° |
| C、60° | D、不能确定 |
若am•a3=a5,则m的值为( )
| A、1 | B、2 | C、3 | D、4 |
在平面直角坐标系xOy中,已知A(1,-1),在y轴确定点P,使△AOP为等腰三角形,则符合条件的点P有( )
| A、2个 | B、3个 | C、4个 | D、5个 |
 已知:右图是二次函数y=(x-m)2+k的图象,其顶点坐标为M(1,-4).
已知:右图是二次函数y=(x-m)2+k的图象,其顶点坐标为M(1,-4).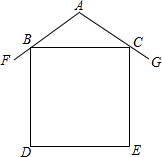 我市新农村建设推动了农村住宅旧貌变新颜,如图所示为一农村民居侧面截图,屋坡AF、AG分别架在墙体的点B、点C处,且AB=AC,侧面四边形BDEC为矩形,若测得∠FAG=100°,则∠FBD=( )
我市新农村建设推动了农村住宅旧貌变新颜,如图所示为一农村民居侧面截图,屋坡AF、AG分别架在墙体的点B、点C处,且AB=AC,侧面四边形BDEC为矩形,若测得∠FAG=100°,则∠FBD=( ) 已知长方形ABCD,AD=6cm,AB=5cm,L、M是CD的中点,N、O、P、Q是AD、BC的三等分点,则阴影部分的面积是
已知长方形ABCD,AD=6cm,AB=5cm,L、M是CD的中点,N、O、P、Q是AD、BC的三等分点,则阴影部分的面积是