Question

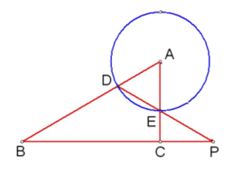
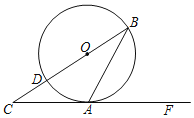
【题目】如图，BD是⊙O的直径，BA是⊙O的弦，过点A的切线CF交BD延长线于点C．

（Ⅰ）若∠C＝25°，求∠BAF的度数；

（Ⅱ）若AB＝AC，CD＝2，求AB的长．

Answer 1

【答案】（Ⅰ）57.5°；（Ⅱ）

【解析】

（Ⅰ）连接OA，AD，根据切线的性质得到OA⊥CF，求得∠OAC＝90°，根据三角形的内角和得到∠COA＝65°，根据等腰三角形的性质得到∠OAB＝32.5°，于是得到结论；

（Ⅱ）根据等腰三角形的性质得到∠B＝∠C，求得∠C＝30°，根据直角三角形的性质得到OA＝OC，于是得到结论．

解：（Ⅰ）连接OA，AD，

∵CF是⊙O的切线，

∴OA⊥CF，

∴∠OAC＝90°，

∵∠C＝25°，

∴∠COA＝65°，

∵∠COA＝∠B＋∠OAB，OA＝OB，

∴∠B＝∠OAB，

∴∠OAB＝32.5°，

∴∠BAF＝∠OAF﹣∠OAB＝90°﹣32.5°＝57.5°；

（Ⅱ）∵AB＝AC，

∴∠B＝∠C，

∵∠COA＝2∠B，

∴3∠C＝90°，

∴∠C＝30°，

∴OA＝OC，

∵OA＝OD，

∴，

∴．