Question

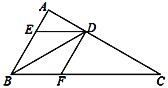
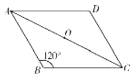
【题目】如图，E是ABCD的BC边的中点，BD与AE相交于F，则△ABF与四边形ECDF的面积之比等于_____．

Answer 1

【答案】

【解析】

△ABF和△ABE等高，先判断出，进而算出，△ABF和

△ AFD等高，得，由，即可解出．

解：∵四边形ABCD为平行四边形，

∴AD∥BC，AD＝BC，

又∵E是ABCD的BC边的中点，

∴，

∵△ABE和△ABF同高，

∴，

∴S△ABE＝S△ABF，

设ABCD中，BC边上的高为h，

∵S△ABE＝×BE×h，SABCD＝BC×h＝2×BE×h，

∴SABCD＝4S△ABE＝4×S△ABF＝6S△ABF，

∵△ABF与△ADF等高，

∴，

∴S△ADF＝2S△ABF，

∴S四边形ECDF＝SABCD﹣S△ABE﹣S△ADF＝S△ABF，

∴，

故答案为： ．