题目内容
5.(1)解不等式组:$\left\{\begin{array}{l}{2x<5}\\{3(x+2)≥x+4}\end{array}\right.$.(2)解方程:$\frac{x}{x-2}$-1=$\frac{4}{x+2}$.
分析 (1)分别求出不等式组中两不等式的解集,找出两解集的公共部分即可;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)$\left\{\begin{array}{l}{2x<5①}\\{3(x+2)≥x+4②}\end{array}\right.$,
由①得:x<$\frac{5}{2}$,
由②得:x≥-1,
∴原不等式组解集为-1≤x<$\frac{5}{2}$;
(2)去分母得:x2+2x-x2+4=4x-8,
解得:x=6,
经检验:x=6 是分式方程的根.
点评 此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
20.若分式$\frac{x}{x+3}$有意义,则x应满足的条件是( )
| A. | x≠0 | B. | x≠-3 | C. | x≥-3 | D. | x≤-3 |
 如图,已知三角形ABC,请用直尺和圆规作出∠B的平分线BD,它与边AC相交于点D,并作出BD的中点E.
如图,已知三角形ABC,请用直尺和圆规作出∠B的平分线BD,它与边AC相交于点D,并作出BD的中点E.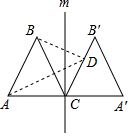 如图,等边三角形△ABC的边长为4,过点C的直线m⊥AC,且△ABC与△A′B′C关于直线m对称,D为线段BC′上一动点,则AD+BD的最小值是8.
如图,等边三角形△ABC的边长为4,过点C的直线m⊥AC,且△ABC与△A′B′C关于直线m对称,D为线段BC′上一动点,则AD+BD的最小值是8. 如图,已知?ABCD,AB>AD,分别以点A,C为圆心,以AD,CB长为半径作弧,交AB,CD于点E,F,连接AF,CE.求证:AF=CE.
如图,已知?ABCD,AB>AD,分别以点A,C为圆心,以AD,CB长为半径作弧,交AB,CD于点E,F,连接AF,CE.求证:AF=CE.