题目内容
若一个直角三角形的两直角边上的中线长分别是3和4，则该直角三角形的斜边长是 ．
考点：勾股定理
专题：
分析：如图，在Rt△ABE与Rt△CBD中，利用勾股定理列出关于a、b的方程组，通过解方程组求得a、b的值；然后在Rt△ABC中根据勾股定理来求斜边AC的长度．
解答：
解：如图，在Rt△ABC中，∠B=90°，AE、CD分别是直角边BC、AB上的中线，且AE=3，CD=4，
则由勾股定理知
，
解得
，
则AB=2a=4，BC=2b=6．
则在Rt△ABC中，根据勾股定理得AC=
=
=2
．
故答案是：2
．
解：如图，在Rt△ABC中，∠B=90°，AE、CD分别是直角边BC、AB上的中线，且AE=3，CD=4，则由勾股定理知
|
解得
|
则AB=2a=4，BC=2b=6．
则在Rt△ABC中，根据勾股定理得AC=
| AB2+BC2 |
| 4a2+4b2 |
| 5 |
故答案是：2
| 5 |
点评：本题考查了勾股定理的运用以及中线的定义，解题的关键是利用整体的数学方法解题．
练习册系列答案
相关题目
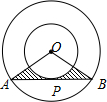如图，两同心圆的圆心为O，大圆的弦AB切小圆于P，两圆的半径分别为6、3，则图中阴影部分的面积是
如图，在平行四边形ABCD中，分别以AB、AD为边向外作等边△ABE、△ADF，延长CB交AE于点G，点G在点A，E之间，连接CE、CF、EF，有下列四个结论：
如图，a∥b，点A在直线a上，点C在直线b上，∠BAC=90°，AB=AC，若∠1=20°，则∠2的度数为