题目内容
8.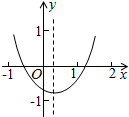 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①a+b+c<0;②a-b+c<0;③b+2a<0;④abc>0,其中所有正确结论的序号是①④.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①a+b+c<0;②a-b+c<0;③b+2a<0;④abc>0,其中所有正确结论的序号是①④.
分析 ①根据当x=1时图象在x轴下方,得出y<0,即a+b+c<0判断即可;
②根据当x=-1时图象在x轴上方,得出y>0,即a-b+c>0判断即可;
③根据对称轴x=-$\frac{b}{2a}$<1,得出2a+b>0进行判断;
④由图象开口向上判断出a>0,由对称轴在y轴右侧得出b<0,由抛物线与y轴交于负半轴,c<0判断即可.
解答 解:①当x=1时图象在x轴下方时,y<0,
即a+b+c<0,①正确;
②当x=-1时图象在x轴上方,y>0,
即a-b+c>0,②错误;
③由抛物线的开口向上知a>0,
∵-$\frac{b}{2a}$<1,
∴2a+b>0,③错误;
④∵图象开口向上,
∴a>0,
∵对称轴在y轴右侧
∴b<0,
∵抛物线与y轴交于负半轴,
∴c<0,
∴abc>0,④正确,
故答案为:①④.
点评 本题考查的是二次函数图象与系数的关系,掌握二次函数y=ax2+bx+c系数符号由抛物线开口方向、对称轴、抛物线与y轴的交点抛物线与x轴交点的个数确定是解题的关键.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
19.$-\frac{1}{6}$的绝对值为( )
| A. | 6 | B. | $-\frac{1}{6}$ | C. | $\frac{1}{6}$ | D. | -6 |
16.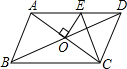 如图,?ABCD的周长为20cm,AC与BD相交于点O,OE⊥AC交AD于E,则△CDE的周长为( )
如图,?ABCD的周长为20cm,AC与BD相交于点O,OE⊥AC交AD于E,则△CDE的周长为( )
 如图,?ABCD的周长为20cm,AC与BD相交于点O,OE⊥AC交AD于E,则△CDE的周长为( )
如图,?ABCD的周长为20cm,AC与BD相交于点O,OE⊥AC交AD于E,则△CDE的周长为( )| A. | 6cm | B. | 8cm | C. | 10cm | D. | 12cm |
17.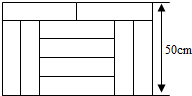 如图,宽为50cm的长方形团由10个形状大小完全相同的小长方形拼成,其汇总一个小长方形的面积为( )
如图,宽为50cm的长方形团由10个形状大小完全相同的小长方形拼成,其汇总一个小长方形的面积为( )
 如图,宽为50cm的长方形团由10个形状大小完全相同的小长方形拼成,其汇总一个小长方形的面积为( )
如图,宽为50cm的长方形团由10个形状大小完全相同的小长方形拼成,其汇总一个小长方形的面积为( )| A. | 400cm2 | B. | 500cm2 | C. | 600cm2 | D. | 4000cm2 |
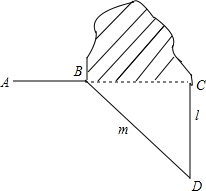 小明爸爸给小明出了一道题:如图,修公路AB遇到一座山,于是要修一条隧道BC.已知A,B,C在同一条直线上,为了在小山的两侧B,C同时施工.过点B作一直线m(在山的旁边经过),过点C作一直线l与m相交于D点,经测量∠ABD=130°,∠D=40°,BD=1000米,CD=800米.若施工队每天挖100米,求施工队几天能挖完?
小明爸爸给小明出了一道题:如图,修公路AB遇到一座山,于是要修一条隧道BC.已知A,B,C在同一条直线上,为了在小山的两侧B,C同时施工.过点B作一直线m(在山的旁边经过),过点C作一直线l与m相交于D点,经测量∠ABD=130°,∠D=40°,BD=1000米,CD=800米.若施工队每天挖100米,求施工队几天能挖完?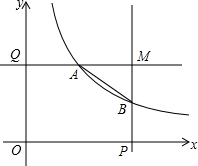 如图,在平面直角坐标系中,P,Q分别是x轴,y轴的正半轴上两动点,OP=2,OQ=k,分别过P,Q作坐标轴的垂线,交反比例函数y=$\frac{k}{x}$于点A,B两垂线交于点M,点E为线段OP上一动点.
如图,在平面直角坐标系中,P,Q分别是x轴,y轴的正半轴上两动点,OP=2,OQ=k,分别过P,Q作坐标轴的垂线,交反比例函数y=$\frac{k}{x}$于点A,B两垂线交于点M,点E为线段OP上一动点.