题目内容
 直角梯形ABCD中,AB∥CD,∠B=90°,AB=4,BC=4
直角梯形ABCD中,AB∥CD,∠B=90°,AB=4,BC=4| 3 |
| 3 |
(1)试说明△ACD为等边三角形.
(2)t为何值时,以P为圆心,PQ长为半径的圆与直线l相切?
(3)求梯形ABCD与直线l在运动过程中所扫过的区域的重叠部分的面积S(用含t的代数式表示).
考点:圆的综合题
专题:
分析:(1)由∠B=90°,AB=4,BC=4
,CD=8.易求得AC=CD=8,∠ACD=60°,即可证得△ACD为等边三角形.
(2)首先连接PQ,作PH⊥AB于H,易求得PQ=4-t,证得四边形PHBQ是矩形,然后设直线l与AC的垂足为E,若⊙P与l相切,则PE=PQ,即可得2t+(4-t)+2t=8或2t+2t-(4-t)=8,继而求得答案;
(3)分别从当0≤t≤2时,当2≤t≤3时,当3≤t≤4时去分析求解即可求得答案.
| 3 |
(2)首先连接PQ,作PH⊥AB于H,易求得PQ=4-t,证得四边形PHBQ是矩形,然后设直线l与AC的垂足为E,若⊙P与l相切,则PE=PQ,即可得2t+(4-t)+2t=8或2t+2t-(4-t)=8,继而求得答案;
(3)分别从当0≤t≤2时,当2≤t≤3时,当3≤t≤4时去分析求解即可求得答案.
解答:解:(1)∵在Rt△ABC中,AB=4,BC=4
,
∴tan∠ACB=
=
,
∴∠ACB=30°,
∴AC=2AB=8,
∵AB∥CD,CD=8,
∴∠BCD=90°,AC=CD,
∴∠ACD=60°,
∴△ACD为等边三角形.
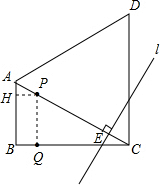 (2)连接PQ,作PH⊥AB于H,
(2)连接PQ,作PH⊥AB于H,
∵∠B=90°,∠ACB=30°,
∴PH∥BQ,∠BAC=60°,
在Rt△APH中,∠APH=30°,AP=2t,
∴AH=AP•cos60°=t,PH=AP•sin60°=
t,
∵BQ=
t,
∴PH=BQ,
∴四边形PHBQ是矩形,
∴PQ=BH=4-t,
设直线l与AC的垂足为E,若⊙P与l相切,则PE=PQ,
∵CE=2t,AC=AP+PE+CE或AC=AP+CE-PE,
即2t+(4-t)+2t=8或2t+2t-(4-t)=8,
解得:t=
或t=
;
(3)设直线l在运动过程中,与CD与AD的交点为M,与BC,AB的交点为N,与AC的交点为E,
当直线过点D时,
∵CD=8,∠ACD=60°,CE=2t,
∴CD=2CE=4t=8,
∴t=2;
当直线l过点B时,CN=
=
t=4
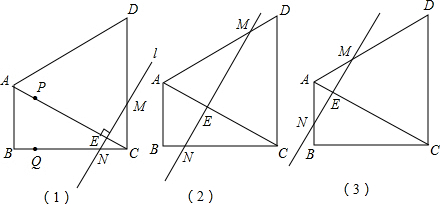
,
∴t=3;
当直线l过点A时,2t=8,
∴t=4;
①如图(1),当0≤t≤2时,在Rt△CEN中,CN=
t,
在Rt△CEM中,CM=2CE=4t,
∴S=
CN•CM=
×
t×4t=
t2;
②如图(2),当2≤t≤3时,
∵AE=AC-CE=8-2t,
∴EM=
(8-2t),EN=
t,
∴S△AEM=
AE•EM=
×
(8-2t)•(8-2t)=2
(4-t)2,S△ACD=16
,S△CEN=
CE•EN=
t2,
∴S=S△ACD-S△AEM+S△CEN=-
t2+16
t-16
;
③当3≤t≤4时,
∵S△AEM=2
(4-t)2,S△AEN=
AE•EN=
×(8-2t)×
(8-2t)=2
(4-t)2,S梯形ABCD=
(AB+CD)•BC=24
,
∴S=S梯形ABCD-S△AEM-S△AEN=-4
t2+32
t-40
.
| 3 |
∴tan∠ACB=
| AB |
| BC |
| ||
| 3 |
∴∠ACB=30°,
∴AC=2AB=8,
∵AB∥CD,CD=8,
∴∠BCD=90°,AC=CD,
∴∠ACD=60°,
∴△ACD为等边三角形.
 (2)连接PQ,作PH⊥AB于H,
(2)连接PQ,作PH⊥AB于H,∵∠B=90°,∠ACB=30°,
∴PH∥BQ,∠BAC=60°,
在Rt△APH中,∠APH=30°,AP=2t,
∴AH=AP•cos60°=t,PH=AP•sin60°=
| 3 |
∵BQ=
| 3 |
∴PH=BQ,
∴四边形PHBQ是矩形,
∴PQ=BH=4-t,
设直线l与AC的垂足为E,若⊙P与l相切,则PE=PQ,
∵CE=2t,AC=AP+PE+CE或AC=AP+CE-PE,
即2t+(4-t)+2t=8或2t+2t-(4-t)=8,
解得:t=
| 4 |
| 3 |
| 12 |
| 5 |
(3)设直线l在运动过程中,与CD与AD的交点为M,与BC,AB的交点为N,与AC的交点为E,
当直线过点D时,
∵CD=8,∠ACD=60°,CE=2t,
∴CD=2CE=4t=8,
∴t=2;
当直线l过点B时,CN=
| CE |
| cos30° |
4
| ||
| 3 |
| 3 |

∴t=3;
当直线l过点A时,2t=8,
∴t=4;
①如图(1),当0≤t≤2时,在Rt△CEN中,CN=
4
| ||
| 3 |
在Rt△CEM中,CM=2CE=4t,
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
4
| ||
| 3 |
8
| ||
| 3 |
②如图(2),当2≤t≤3时,
∵AE=AC-CE=8-2t,
∴EM=
| 3 |
2
| ||
| 3 |
∴S△AEM=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 1 |
| 2 |
2
| ||
| 3 |
∴S=S△ACD-S△AEM+S△CEN=-
4
| ||
| 3 |
| 3 |
| 3 |
③当3≤t≤4时,
∵S△AEM=2
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
∴S=S梯形ABCD-S△AEM-S△AEN=-4
| 3 |
| 3 |
| 3 |
点评:此题考查了切线的性质、等边三角形的判定与性质、三角函数的性质以及矩形的判定与性质等知识.此题综合性较强,注意掌握辅助线的作法,注意数形结合思想、分类讨论思想与方程思想的应用.

练习册系列答案
相关题目
下列四个数中,是负数的是( )
| A、|-1| | ||
| B、-(-1) | ||
| C、-1 | ||
D、
|
 如图,△ABC内接于⊙O,D为AB延长线上一点.若∠CBD=130°,则∠AOC的大小为( )
如图,△ABC内接于⊙O,D为AB延长线上一点.若∠CBD=130°,则∠AOC的大小为( )| A、65° | B、100° |
| C、110° | D、130° |
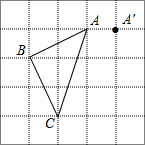 如图,在边长均为1cm的正方形网格中,△ABC的三个顶点和点A′均在格点上.将△ABC向右平移,使点A平移至点A′处,得到△A′B′C′.在图中画出△A′B′C′,并求边AC扫过的图形面积.
如图,在边长均为1cm的正方形网格中,△ABC的三个顶点和点A′均在格点上.将△ABC向右平移,使点A平移至点A′处,得到△A′B′C′.在图中画出△A′B′C′,并求边AC扫过的图形面积.