题目内容
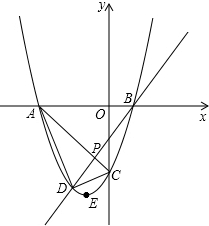 如图,在平面直角坐标系中,点B的坐标(1,0),OA=OC=3OB,抛物线经过A、B、C三点,记抛物线顶点为点E.
如图,在平面直角坐标系中,点B的坐标(1,0),OA=OC=3OB,抛物线经过A、B、C三点,记抛物线顶点为点E.(1)A(
(2)求抛物线的解析式及E点坐标;
(3)若点P为线段AC上的一个动点(不与A、C重合),直线PB与抛物线交于点D,连接DA,DC.
①计算△ACE的面积;
②是否存在点D,使得S△ADC=
| 1 |
| 2 |
(4)在(3)的条件下,当△PBC为等腰三角形时,直接写出点P的坐标.
考点:二次函数综合题
专题:
分析:(1)根据OA=OC=3OB,可得OA、OC的长度,根据线段的长度,可得点的坐标;
(2)根据待定系数法,可得抛物线的解析式,根据解析式,可得顶点坐标;
(3)①根据角的和差,可得∠ACE的度数,根据三角形的面积公式,可得答案;
②根据等底三角形面积的关系,可得三角形高之间的关系,可得答案;
(4)根据等腰三角形的判定,分类讨论:PB=PC,PB=BC,PC=BC,可得答案.
(2)根据待定系数法,可得抛物线的解析式,根据解析式,可得顶点坐标;
(3)①根据角的和差,可得∠ACE的度数,根据三角形的面积公式,可得答案;
②根据等底三角形面积的关系,可得三角形高之间的关系,可得答案;
(4)根据等腰三角形的判定,分类讨论:PB=PC,PB=BC,PC=BC,可得答案.
解答:解:(1)由点B的坐标(1,0),OA=OC=3OB,得
OA=OC=3,.
A(-3,0),C( 0,-3);
(2)设抛物线的解析式y=ax2+bx+c,函数图象经过点A、B、C,得
,解得
,
抛物线的解析式为y=x2+2x-3,
顶点坐标是x=-
=-
=-1,y=
=
=-4,
E(-1,-4);
(3)①由题意可知∠ACO=45°,CE与y轴的负半轴所成的角也为45°,
∴∠ACE=90°,AC=3
,CE=
∴S△ACE=
AC•CE=
×3
×
=2;
②存在存在点D,使得S△ADC=
S△ACE,
D到AC的距离为CE的一半,
设D(x,x2+2x-3),直线AC的解析式为y=-x-3,即y+x+3=0,
D到AC的距离为
=
,
解得x1=
,y1=x2+2x-3=
,
x2=
,y2=
;
D(
,
),D(
,
);
(4)设P(x,-x-3),BC=
=
,
①当PB=PC时,
=
,
化简,得
4x=-13.
解得x=-
,y=-x-3=
,p(-
,
);
②当PB=BC时,
=
,
化简,得2x2+4x=0.
解得x=-2或x=0(不符合题意的要舍去),y=-x-3=-(-2)-3=-1,P(-2,-1);
③当PC=BC时,
=
,
化简,得x2+6x+13=0,△=b2-4ac=62-4×1×13=-16,方程无实数根;
当△PBC为等腰三角形时,点P的坐标(-
,
),(-2,-1).
OA=OC=3,.
A(-3,0),C( 0,-3);
(2)设抛物线的解析式y=ax2+bx+c,函数图象经过点A、B、C,得
|
|
抛物线的解析式为y=x2+2x-3,
顶点坐标是x=-
| b |
| 2a |
| 2 |
| 2×1 |
| 4ac-b2 |
| 4a |
| 4×1×(-3)-22 |
| 4×1 |
E(-1,-4);
(3)①由题意可知∠ACO=45°,CE与y轴的负半轴所成的角也为45°,
∴∠ACE=90°,AC=3
| 2 |
| 2 |
∴S△ACE=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
②存在存在点D,使得S△ADC=
| 1 |
| 2 |
D到AC的距离为CE的一半,
设D(x,x2+2x-3),直线AC的解析式为y=-x-3,即y+x+3=0,
D到AC的距离为
| |x+x2+2x-3| | ||
|
| ||
| 2 |
解得x1=
-3+
| ||
| 2 |
-5-
| ||
| 2 |
x2=
-3-
| ||
| 2 |
-5+
| ||
| 2 |
D(
-3+
| ||
| 2 |
-5-
| ||
| 2 |
-3-
| ||
| 2 |
-5+
| ||
| 2 |
(4)设P(x,-x-3),BC=
| OB2+OC2 |
| 10 |
①当PB=PC时,
| (x-1)2+(-x-3-0)2 |
| (x-0)2+(-x-3-3)2 |
化简,得
4x=-13.
解得x=-
| 13 |
| 4 |
| 1 |
| 4 |
| 13 |
| 4 |
| 1 |
| 4 |
②当PB=BC时,
| (x-1)2+(-x-3)2 |
| 10 |
化简,得2x2+4x=0.
解得x=-2或x=0(不符合题意的要舍去),y=-x-3=-(-2)-3=-1,P(-2,-1);
③当PC=BC时,
| (x-0)2+(-x-3-3)2 |
| 10 |
化简,得x2+6x+13=0,△=b2-4ac=62-4×1×13=-16,方程无实数根;
当△PBC为等腰三角形时,点P的坐标(-
| 13 |
| 4 |
| 1 |
| 4 |
点评:本题考查了二次函数综合题,利用了待定系数法求函数解析式,等底三角形的面积与高的关系,等腰三角形的判定,分类讨论是解题关键.

练习册系列答案
相关题目
在△ABC中,∠C=90°,若c=29,a=20,则b=( )
| A、9 | B、10 | C、20 | D、21 |