题目内容
【题目】一种火爆的网红电子产品，每件产品成本
元、工厂将该产品进行网络批发，批发单价
（元）与一次性批发量
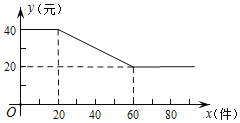
（件）（为正整数）之间满足如图所示的函数关系．
直接写出与之间所满足的函数关系式，并写出自变量的取值范围；
若一次性批发量不超过
件，当批发量为多少件时，工厂获利最大？最大利润是多少？
【答案】（1）当
且
为整数时， 
当
且为整数时， 
;当
且为整数时，
；（2）一次批发
件时所获利润最大，最大利润是
元．
【解析】
（1）根据函数图像，求出各个部分的解析式即可；
（2）设所获利润
（元），分段求出各个不发的利润，再比较最大利润即可求解.
解：
当且为整数时，
当且为整数时， ;
当且为整数时，；
设所获利润（元），
当且为整数时，
元，
当且为整数时，w=480 ,
∴当且为整数时，
当
时，最大，最大值为元．
答：一次批发件时所获利润最大，最大利润是元．
阅读快车系列答案【题目】为迎接“世界华人炎帝故里寻根节”，某工厂接到一批纪念品生产订单，按要求在15天内完成，约定这批纪念品的出厂价为每件20元，设第x天（1≤x≤15，且x为整数）每件产品的成本是p元，p与x之间符合一次函数关系，部分数据如表：
天数（x） | 1 | 3 | 6 | 10 |
每件成本p（元） | 7.5 | 8.5 | 10 | 12 |
任务完成后，统计发现工人李师傅第x天生产的产品件数y（件）与x（天）满足如下关系：y=
，
设李师傅第x天创造的产品利润为W元．
（1）直接写出p与x，W与x之间的函数关系式，并注明自变量x的取值范围：
（2）求李师傅第几天创造的利润最大？最大利润是多少元？
（3）任务完成后．统计发现平均每个工人每天创造的利润为299元．工厂制定如下奖励制度：如果一个工人某天创造的利润超过该平均值，则该工人当天可获得20元奖金．请计算李师傅共可获得多少元奖金？
【题目】某商场为了抓住夏季来临，衬衫热销的契机，决定用46000元购进
、
、
三种品牌的衬衫共300件，并且购进的每一种衬衫的数量都不少于90件.设购进种型号的衬衣
件，购进种型号的衬衣
件，三种品牌的衬衫的进价和售价如下表所示：
型号 |
|
|
|
进价（元/件） | 100 | 200 | 150 |
售价（元/件） | 200 | 350 | 300 |
（Ⅰ）直接用含、的代数式表示购进种型号衬衣的件数，其结果可表示为______；
（Ⅱ）求与之间的函数关系式；
（Ⅲ）如果该商场能够将购进的衬衫全部售出，但在销售这些衬衫的过程中还需要另外支出各种费用共计1000元.
①求利润
（元）与
（件）之间的函数关系式；
②求商场能够获得的最大利润.
