题目内容
16.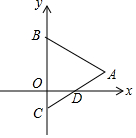 如图,在平面直角坐标系中,点B、C在y轴上,△ABC是等边三角形,AB=4,AC与x轴的交点D为AC边的中点,则点D的坐标为( )
如图,在平面直角坐标系中,点B、C在y轴上,△ABC是等边三角形,AB=4,AC与x轴的交点D为AC边的中点,则点D的坐标为( )| A. | (1,0) | B. | (2$\sqrt{3}$,0) | C. | (2,0) | D. | ($\sqrt{3}$,0) |
分析 先过点A作AE⊥OB,根据△ABC是等边三角形,求出AE,再根据三角形的中位线的性质得到得出点D的坐标.
解答 解:过点A作AE⊥OB,如图:
∵点B、C在y轴上,△ABC是等边三角形,AB=4,
∴AE=2$\sqrt{3}$,
∵OD∥AE,D为AC边的中点,
∴$\frac{OD}{AE}$=$\frac{1}{2}$,
∴OD=$\sqrt{3}$,
∴D($\sqrt{3}$,0).
故选D.
点评 此题考查了等边三角形的性质,用到的知识点是勾股定理,关键是作出辅助线,求出点A的坐标.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
6.据教育部数据显示,2017届全国普通高校毕业生预计795万人.将数据795万用科学记数法可表示为( )
| A. | 79.5×105 | B. | 7.95×106 | C. | 7.95×102 | D. | 0.795×107 |
11.某种商品的进货检为每件a元,零售价为每件90元,若商品按八五折出售,仍可获利10%,则下列方程正确的是( )
| A. | 85%a10%×90 | B. | 90×85%×10%=a | C. | 85%(90-a)=10% | D. | (1+10%)a=90×85% |
1. 数学小组的同学为了解“阅读经典”活动的开展情况,随机调查了50名同学,对他们一周的阅读时间进行了统计,并绘制成如图所示的条形统计图,这组数据的中位数和众数分别是( )
数学小组的同学为了解“阅读经典”活动的开展情况,随机调查了50名同学,对他们一周的阅读时间进行了统计,并绘制成如图所示的条形统计图,这组数据的中位数和众数分别是( )
 数学小组的同学为了解“阅读经典”活动的开展情况,随机调查了50名同学,对他们一周的阅读时间进行了统计,并绘制成如图所示的条形统计图,这组数据的中位数和众数分别是( )
数学小组的同学为了解“阅读经典”活动的开展情况,随机调查了50名同学,对他们一周的阅读时间进行了统计,并绘制成如图所示的条形统计图,这组数据的中位数和众数分别是( )| A. | 中位数和众数都是8小时 | B. | 中位数是25人,众数是20人 | ||
| C. | 中位数是13人,众数是20人 | D. | 中位数是6小时,众数是8小时 |
5.计算(-6)÷(-3)的结果是( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | -2 | D. | 3 |
 过⊙O上任意一点B作过圆心O的直线交⊙O于另一点E,点A为BE延长线上任意一点,过点A作⊙O的切线AB,切点为点D,过B作BC⊥AD于C,BC交⊙O于点F,连BD
过⊙O上任意一点B作过圆心O的直线交⊙O于另一点E,点A为BE延长线上任意一点,过点A作⊙O的切线AB,切点为点D,过B作BC⊥AD于C,BC交⊙O于点F,连BD 如图,在正方体的一角截去一个小正方体,所得立体图形的主视图是( )
如图,在正方体的一角截去一个小正方体,所得立体图形的主视图是( )


