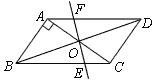
题目内容
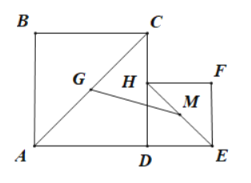
【题目】如图1,在矩形![]() 中,
中,![]() ,延长
,延长![]() 至点
至点![]() ,使得
,使得![]() 过点
过点![]() 作
作![]() ,交线段
,交线段![]() 于点
于点![]() .设
.设![]()

(1)连结![]() ,请求出
,请求出![]() 的度数和
的度数和![]() 的半径(用
的半径(用![]() 的代数式表示). (直接写出答案)
的代数式表示). (直接写出答案)
(2)证明:点![]() 是
是![]() 的中点.
的中点.
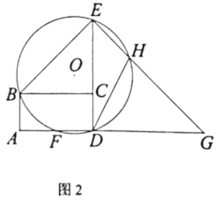
(3)如图2,延长![]() 至点
至点![]() ,使得
,使得![]() , 连结
, 连结![]() ,交
,交![]() 于点
于点![]()
①连结![]() ,当
,当![]() 与四边形
与四边形![]() 其它三边中的一边相等时,请求出所有满足条件的
其它三边中的一边相等时,请求出所有满足条件的![]() 的值.
的值.
②当点![]() 关于直线
关于直线![]() 对称点
对称点![]() 恰好落在
恰好落在![]() 上,连结
上,连结![]() .记
.记![]() 和
和![]() 的面积分别为
的面积分别为![]() ,请直接写出
,请直接写出![]() 的值.
的值.
【答案】(1)90°,![]() ;(2)详见解析;(3)①
;(2)详见解析;(3)①![]() ,或
,或![]() ,或
,或![]() ;②
;②![]()
【解析】
(1)利用圆心角与圆周角的关系可得到:∠BOD=2∠BED=2×45°=90°,再通过构造全等三角形,最后利用勾股定理求解即可;
(2)连结![]() ,利用勾股定理计算得到
,利用勾股定理计算得到![]() 从而求解
从而求解![]() 可得结论,
可得结论,
(3)①要分三种情况进行分类讨论:DH=BD或DH=BE或DH=EH,可得答案. ②利用对称性质,相似三角形性质求得BD、DC、DE、DH的值,作G′P⊥GE,DQ⊥GE,利用同底三角形面积之比等于高之比求得:![]() 利用
利用![]() 进行转化,可得答案.
进行转化,可得答案.
解:(1)如图1,过点O作OM⊥AD于M交BC于N,
∵ABCD是矩形,AB=x,AD=2AB
∴AB=CD=x,BC=AD=2x,∠A=∠ADC=∠BCD=∠ABC=∠BCE=90°,BC∥AD
∵CE=BC
∴∠BED=∠CBE=45°
∴∠BOD=2∠BED=2×45°=90°
∴∠BON+∠DOM=90°
∵OM⊥AD,BC∥AD
∴OM⊥BC
∴∠AMO=∠OMD=∠BNO=90°
∴∠ODM+∠DOM=90°
∴∠BON=∠ODM,
∵OB=OD,
∴△BON≌△ODM(AAS)
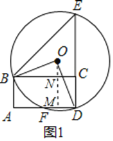
∴BN=OM,ON=DM
∵∠A=∠ABC=∠AMO=90°
∴ABNM是矩形
∴AM=BN,MN=AB=x
∴AD=AM+DM=OM+DM=MN+2DM,
即:2x=x+2DM,DM= ![]() x
x
∴OM=MN+ON=MN+DM=![]()
∴OD=![]()
即⊙O的半径为![]()
![]() 如图1,连结
如图1,连结![]() ,
,
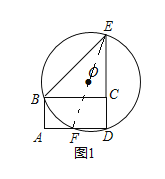
在矩形![]() 中
中
![]()
![]() 为
为![]() 的直径,
的直径,![]()
![]()
![]()
![]()
![]()
![]() 点
点![]() 是
是![]() 的中点.
的中点.
(3)①如图2,当![]() 时,
时,
![]()
![]()
![]()
![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]()
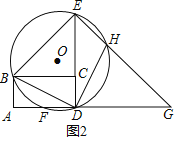
如图2,当![]() 时,
时,![]()
![]()
![]()
![]()
![]()
经检验:![]() 是原方程的根,且符合题意.
是原方程的根,且符合题意.
如图3,连结![]() 当
当![]() 时,
时,
![]()
![]()
![]()
![]()
![]()
![]()
![]() 为
为![]() 的中位线,
的中位线,
![]()
![]()
![]()
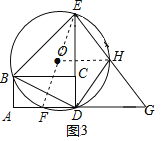
综上:,当![]() 与四边形
与四边形![]() 其它三边中的一边相等时,
其它三边中的一边相等时, ![]() 的值为
的值为![]() 或
或![]() 或
或![]() .
.
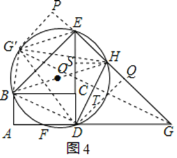
②如图4,过D作DQ⊥GE于Q,过G′作G′P⊥GE延长线于P,
连接GG′、G′B、G′E、G′H、G′D,GG′交DH于T,
∵G,G′关于DH对称,
∴GG′⊥DH,GG′=2GT,
∠HG′D=∠HGD,
∵∠HG′D=∠HED,
∴∠HED=∠HGD=45°
∴DG=DE,
即:10-x=3x,解得:x=![]() ,
,
由①知:此时,BD=DH=![]() ,直径BH=
,直径BH=![]() ,
,
DG=DG′=DE=![]() ,HS=ES=
,HS=ES=![]()
∵∠BDC+∠EDH=∠EDH+∠GDT=90°,
∴∠BDC=∠GDT
∴△BDC∽△GDT
∴ 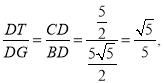
∴DT=![]() ,TG=TG′=
,TG=TG′=![]()
TH=DH-DT= ![]()
GH= ![]()
∵G′P⊥GE
∴∠P=∠GTH=90°,∠HGT=∠G′GP
∴△GG′P∽△GHT
∴ ![]() 即:
即:![]()
解得:G′P=![]()
∵DQGH=GTDH,
即:![]()
解得:DQ=![]()
∴ 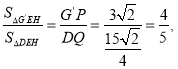
![]()
![]()
∴ ![]()
∴G′E∥BH
∴S△BEG′=S△G′EH
∴![]()
即:![]()

 黄冈小状元同步计算天天练系列答案
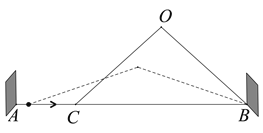
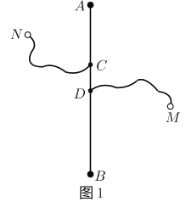
黄冈小状元同步计算天天练系列答案【题目】如图1,长度为6千米的国道![]() 两侧有
两侧有![]() ,
,![]() 两个城镇,从城镇到公路分别有乡镇公路连接,连接点为
两个城镇,从城镇到公路分别有乡镇公路连接,连接点为![]() 和
和![]() ,其中
,其中![]() 、
、![]() 之间的距离为2千米,
之间的距离为2千米,![]() 、
、![]() 之间的距离为1千米,
之间的距离为1千米,![]() 、
、![]() 之间的乡镇公路长度为2.3千米,
之间的乡镇公路长度为2.3千米,![]() 、
、![]() 之间的乡镇公路长度为3.2千米,为了发展乡镇经济,方便两个城镇的物资输送,现需要在国道
之间的乡镇公路长度为3.2千米,为了发展乡镇经济,方便两个城镇的物资输送,现需要在国道![]() 上修建一个物流基地
上修建一个物流基地![]() ,设
,设![]() 、
、![]() 之间的距离为
之间的距离为![]() 千米,物流基地
千米,物流基地![]() 沿公路到
沿公路到![]() 、
、![]() 两个城镇的距离之和为
两个城镇的距离之和为![]() 干米,以下是对函数
干米,以下是对函数![]() 随自变量
随自变量![]() 的变化规律进行的探究,请补充完整.
的变化规律进行的探究,请补充完整.
(1)通过取点、画图、测量,得到![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| 10.5 | 8.5 | 6.5 | 10.5 | 12.5 |
(2)如图2,建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.
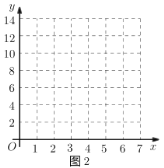
(3)结合画出的函数图象,解决问题:
①若要使物流基地![]() 沿公路到
沿公路到![]() 、
、![]() 两个城镇的距离之和最小,则物流基地
两个城镇的距离之和最小,则物流基地![]() 应该修建在何处?(写出所有满足条件的位置)
应该修建在何处?(写出所有满足条件的位置)
答:__________.
②如右图,有四个城镇![]() 、
、![]() 、
、![]() 、
、![]() 分别位于国道
分别位于国道![]() 两侧,从城镇到公路分别有乡镇公路连接,若要在国道上修建一个物流基地
两侧,从城镇到公路分别有乡镇公路连接,若要在国道上修建一个物流基地![]() ,使得
,使得![]() 沿公路到
沿公路到![]() 、
、![]() 、
、![]() 、
、![]() 的距离之和最小,则物流基地
的距离之和最小,则物流基地![]() 应该修建在何处?(写出所有满足条件的位置)
应该修建在何处?(写出所有满足条件的位置)
答:__________.

【题目】参照学习函数的过程方法,探究函数![]() 的图像与性质,因为
的图像与性质,因为![]() ,即
,即![]() ,所以我们对比函数
,所以我们对比函数![]() 来探究列表:
来探究列表:
| … | -4 | -3 | -2 | -1 |
|
| 1 | 2 | 3 | 4 | … | |
| … |
|
| 1 | 2 | 4 | -4 | -2 | -1 |
|
| … | |
| … |
|
| 2 | 3 | 5 | -3 | -2 | 0 |
|
| … |
描点:在平面直角坐标系中以自变量![]() 的取值为横坐标,以
的取值为横坐标,以![]() 相应的函数值为纵坐标,描出相应的点如图所示:
相应的函数值为纵坐标,描出相应的点如图所示:
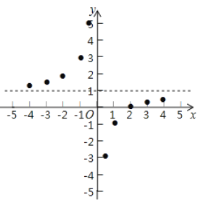
(1)请把![]() 轴左边各点和右边各点分别用一条光滑曲线,顺次连接起来;
轴左边各点和右边各点分别用一条光滑曲线,顺次连接起来;
(2)观察图象并分析表格,回答下列问题:
①当![]() 时,
时,![]() 随
随![]() 的增大而______;(“增大”或“减小”)
的增大而______;(“增大”或“减小”)
②![]() 的图象是由
的图象是由![]() 的图象向______平移______个单位而得到的;
的图象向______平移______个单位而得到的;
③图象关于点______中心对称.(填点的坐标)
(3)函数![]() 与直线
与直线![]() 交于点
交于点![]() ,
,![]() ,求
,求![]() 的面积.
的面积.