Question

【题目】参照学习函数的过程方法，探究函数的图像与性质，因为，即，所以我们对比函数来探究列表：

	…	-4	-3	-2	-1			1	2	3	4	…
	…			1	2	4	-4	-2	-1			…
	…			2	3	5	-3	-2	0			…

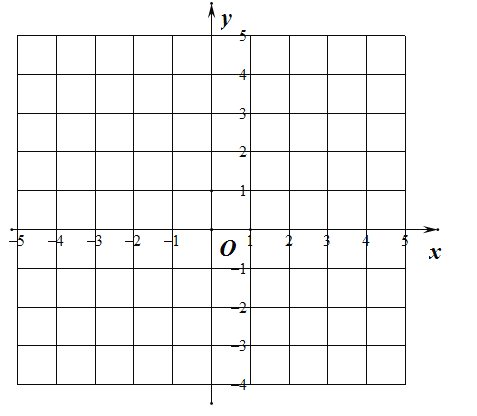
描点：在平面直角坐标系中以自变量的取值为横坐标，以相应的函数值为纵坐标，描出相应的点如图所示：

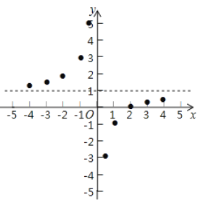
（1）请把轴左边各点和右边各点分别用一条光滑曲线，顺次连接起来；

（2）观察图象并分析表格，回答下列问题：

①当时，随的增大而______；（“增大”或“减小”）

②的图象是由的图象向______平移______个单位而得到的；

③图象关于点______中心对称.（填点的坐标）

（3）函数与直线交于点，，求的面积.

Answer 1

【答案】（1）如图所示，见解析；（2）①增大；②上，1；③；（3）1.

【解析】

（1）按要求把轴左边点和右边各点分别用一条光滑曲线顺次连接起来即可；

（2）①观察图像可得出函数增减性；②由表格数据及图像可得出平移方式；③由图像可知对称中心；

（3）将与联立求解，得到A、B两点坐标，将△AOB分为△AOC与△BOC计算面积即可.

（1）如图所示：

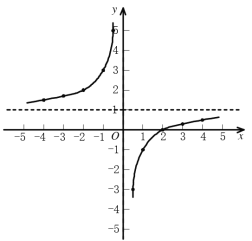
（2）①由图像可知：当时，随的增大而增大，故答案为：增大；

②由表格数据及图像可知，的图象是由的图象向上平移1个单位而得到的，故答案为：上，1；

③由图像可知图像关于点（0,1）中心对称.

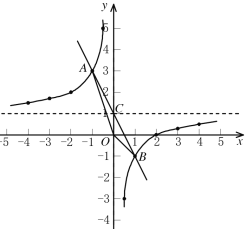
（3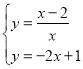），解得：或

∴A点坐标为（-1,3），B点坐标为（1，-1）

设直线与y轴交于点C，当x=0时，y=1，

所以C点坐标为（0,1），如图所示，

S△AOB= S△AOC+ S△BOC

=

=

=

所以△AOB的面积为1.