题目内容
 两个反比例函数y=
两个反比例函数y= ,y=
,y= 在第一象限内的图象如图所示.点P1,P2,P3、…、P2007在反比例函数y=
在第一象限内的图象如图所示.点P1,P2,P3、…、P2007在反比例函数y= 上,它们的横坐标分别为x1、x2、x3、…、x2007,纵坐标分别是1,3,5…共2007个连续奇数,过P1,P2,P3、…、P2007分别作y轴的平行线,与y=
上,它们的横坐标分别为x1、x2、x3、…、x2007,纵坐标分别是1,3,5…共2007个连续奇数,过P1,P2,P3、…、P2007分别作y轴的平行线,与y= 的图象交点依次为Q1(x1′,y1′)、Q1(x2′,y2′)、…、Q2(x2007′,y2007′),
的图象交点依次为Q1(x1′,y1′)、Q1(x2′,y2′)、…、Q2(x2007′,y2007′),则|P2007Q2007|= .
【答案】分析:要求出|P2007Q2007|的值,就要先求|Qy2007-Py2007|的值,因为纵坐标分别是1,3,5 …,共2007个连续奇数,其中第2007个奇数是2×2007-1=4013,所以P2007的坐标是(Px2007,4013),那么可根据P点都在反比例函数y= 上,可求出此时Px2007的值,那么就能得出P2007的坐标,然后将P2007的横坐标代入y=
上,可求出此时Px2007的值,那么就能得出P2007的坐标,然后将P2007的横坐标代入y= 中即可求出Qy2007的值.那么|P2007Q2007|=|Qy2007-Py2007|,由此可得出结果.
中即可求出Qy2007的值.那么|P2007Q2007|=|Qy2007-Py2007|,由此可得出结果.
解答:解:由题意可知:P2007的坐标是(Px2007,4013),
又∵P2007在y= 上,
上,
∴Px2007= .
.
而Qx2007(即Px2007)在y= 上,所以Qy2007=
上,所以Qy2007= =
= =
= ,
,
∴|P2007Q2007|=|Py2007-Qy2007|=|4013- |=
|= .
.
故答案为: .
.
点评:本题的关键是找出P点纵坐标的规律,以这个规律为基础求出P2007的横坐标,进而求出Q2007的值,从而可得出所求的结果.
 上,可求出此时Px2007的值,那么就能得出P2007的坐标,然后将P2007的横坐标代入y=
上,可求出此时Px2007的值,那么就能得出P2007的坐标,然后将P2007的横坐标代入y= 中即可求出Qy2007的值.那么|P2007Q2007|=|Qy2007-Py2007|,由此可得出结果.
中即可求出Qy2007的值.那么|P2007Q2007|=|Qy2007-Py2007|,由此可得出结果.解答:解:由题意可知:P2007的坐标是(Px2007,4013),
又∵P2007在y=
 上,
上,∴Px2007=
 .
.而Qx2007(即Px2007)在y=
 上,所以Qy2007=
上,所以Qy2007= =
= =
= ,
,∴|P2007Q2007|=|Py2007-Qy2007|=|4013-
 |=
|= .
.故答案为:
 .
.点评:本题的关键是找出P点纵坐标的规律,以这个规律为基础求出P2007的横坐标,进而求出Q2007的值,从而可得出所求的结果.

练习册系列答案
相关题目
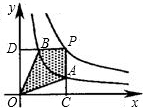 ,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,下列说法正确的是( )
,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,下列说法正确的是( ) 如图,两个反比例函数
如图,两个反比例函数
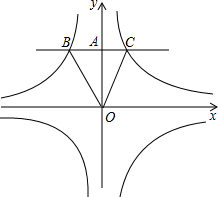 如图,已知反比例函数y=
如图,已知反比例函数y= 已知两个反比例函数
已知两个反比例函数