题目内容
16.如图1,AB∥CD,EOF是直线AB、CD间的一条折线.(1)试证明:∠O=∠BEO+∠DFO.
(2)如果将折一次改为折二次,如图2,则∠BEO、∠O、∠P、∠PFC之间会满足怎样的数量关系,证明你的结论.
(3)如果将折一次改为折三次,如图3,则∠BEO、∠O、∠P、∠Q、∠QFD之间会满足怎样的数量关系(直接写出结果不需证明)

分析 (1)根据平行线的性质求出∠EOM=∠BEO,∠FOM=∠DFO,即可得出答案;
(2)根据平行线的性质得出∠1=∠BEO,∠2=∠3,∠4=∠PFC,相加即可得出答案;
(3)根据平行线的性质得出∠1=∠BEO,∠2=∠3,∠4=∠5,∠6=∠DFQ,相加即可得出答案.
解答 (1)证明:作OM∥AB,如图1,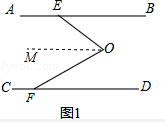
∴∠EOM=∠BEO,
∵AB∥CD,
∴OM∥CD,
∴∠FOM=∠DFO,
∴∠EOM+∠FOM=∠BEO+∠DFO,
即:∠EOF=∠BEO+∠DFO;
(2)∠O+∠PFC=∠BEO+∠P,
证明:作OM∥AB,PN∥CD,如图2,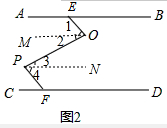
∵AB∥CD,
∴OM∥PN∥AB∥CD,
∴∠1=∠BEO,∠2=∠3,∠4=∠PFC,
∴∠1+∠2+∠PFC=∠BEO+∠3+∠4,
∴∠O+∠PFC=∠BEO+∠P;
(3)解:∠O+∠Q=∠BEO+∠P+∠QFD,
理由是: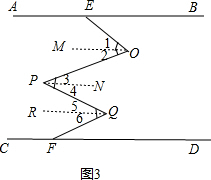
作OM∥AB,PN∥CD,QR∥AB,如图3,
∵AB∥CD,
∴OM∥PN∥∥QR∥AB∥CD,
∴∠1=∠BEO,∠2=∠3,∠4=∠5,∠6=∠DFQ,
∴∠1+∠2+∠5+∠6=∠BEO+∠3+∠4+∠DFQ,
∴∠EOP+∠PFC=∠BEO+∠OPQ.
点评 本题考查了平行线的性质的应用,能正确作出辅助线是解此题的关键,注意:两直线平行,内错角相等.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
11.计算($\frac{{a}^{2}b}{a-b}$)3的结果是( )
| A. | $\frac{{a}^{5}b}{(a-b)^{3}}$ | B. | $\frac{{a}^{6}{b}^{3}}{{a}^{3}-{b}^{3}}$ | C. | $\frac{{a}^{6}{b}^{3}}{(a-b)^{3}}$ | D. | $\frac{{a}^{5}{b}^{3}}{{a}^{3}-{b}^{3}}$ |
 如图:已知:△ABC中,∠ABC、∠BCA的平分线,交于点O,过点O画EF∥BC交AB于点E,AC于点F;写出图中相等的线段,并说明理由.
如图:已知:△ABC中,∠ABC、∠BCA的平分线,交于点O,过点O画EF∥BC交AB于点E,AC于点F;写出图中相等的线段,并说明理由. 如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是54cm2,AB=15cm,AC=12cm,求DE的长.
如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是54cm2,AB=15cm,AC=12cm,求DE的长.