题目内容
如图，点E、F分别是□ABCD的边BC、AD上的点，且BE=DF．
（1） 求证：四边形AECF是
平行四边形；
（2） 若AE=BE，∠BAC＝90°，试判断四边形AECF的形状，并说明理由．
(1) 证明：在平行四边形ABCD中，AD//BC且AD=BC，（1分）
因BE=DF，所以AF=CE
\AF=CE且AF//CE
\四边形AECF是平行四边形．（3分）
(2) 猜想： 四边形AECF是菱形 （4分）
证明：∵AE=BE，\ÐEAB=ÐEBA
∵ÐBAC=900，\ÐCBA+ÐBCA=Ð=900．
\ÐEAC=ÐBAC
\AE=BE=CE （5分）
\四边形AECF是菱形． （6分）
练习册系列答案
相关题目
CD于点F.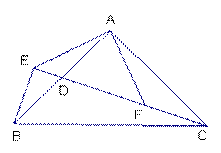
，
，
，0.3030030003，− 
，3.14中，无理数的个数是 ( )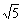
、
、
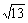，求这个三角形BC边上的高．
．
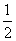和7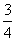
，求A、B两点的距离.