题目内容
20.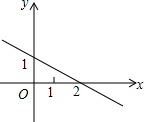 若函数y=kx+b(k,b为常数)的图象如图所示,那么当y>0时,x的取值范围是( )
若函数y=kx+b(k,b为常数)的图象如图所示,那么当y>0时,x的取值范围是( )| A. | x>2 | B. | x<2 | C. | x<1 | D. | x>1 |
分析 一次函数的y=kx+b图象经过点(2,0),由函数表达式可得,kx+b>0其实就是一次函数的函数值y>0,结合图象可以看出答案.
解答 解:由图可知:当x2时,y>0,即kx+b>0;
因此y=kx+b>0的解集为:x<2,
故选B.
点评 本题考查了数形结合的数学思想,即学生利用图象解决问题的方法,这也是一元一次不等式与一次函数知识的具体应用.易错易混点:学生往往由于不理解不等式与一次函数的关系或者不会应用数形结合,盲目答题,造成错误.

练习册系列答案
相关题目
10.2015羊年春晚在某网站取得了同时在线人数超14 000 000的惊人成绩,创下了全球单平台网络直播记录,则14 000 000用科学记数法可表示为( )
| A. | 0.14×108 | B. | 1.4×107 | C. | 1.4×108 | D. | 14×106 |
15.若关于x的一元一次不等式组$\left\{\begin{array}{l}{3-2x>1}\\{x-a>0}\end{array}\right.$恰有3个整数解,那么a的取值范围是( )
| A. | -2<a<1 | B. | -3<a≤-2 | C. | -3≤a<-2 | D. | -3<a<-2 |
5.学校建围栏,要为24000根栏杆油漆,由于改进了技术,每天比原计划多油400根,结果提前两天完成了任务,请问原计划每天油多少根栏杆?如果设原计划每天油x根栏杆,根据题意列方程为( )
| A. | $\frac{24000}{x}$=$\frac{24000}{x-400}$+2 | B. | $\frac{24000}{x}$=$\frac{24000}{x-400}$-2 | ||
| C. | $\frac{24000}{x}$=$\frac{24000}{x+400}$-2 | D. | $\frac{24000}{x}$=$\frac{24000}{x+400}$+2 |
9.将多项式a2+6a-16因式分解正确的是( )
| A. | (a-2)(a-8) | B. | (a+2)(a-8) | C. | (a-2)(a+8) | D. | (a+2)(a+8) |
10. 如图所示,D,E分别是△ABC的边AC、BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数为( )
如图所示,D,E分别是△ABC的边AC、BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数为( )
 如图所示,D,E分别是△ABC的边AC、BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数为( )
如图所示,D,E分别是△ABC的边AC、BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
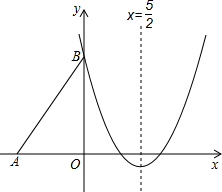 如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=$\frac{2}{3}$x2+bx+c经过点B,且顶点在直线x=$\frac{5}{2}$上.
如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=$\frac{2}{3}$x2+bx+c经过点B,且顶点在直线x=$\frac{5}{2}$上.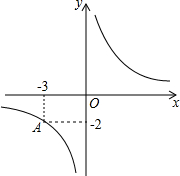 如图,已知反比例函数y=$\frac{k}{x}$的图象经过点A(-3,-2).
如图,已知反比例函数y=$\frac{k}{x}$的图象经过点A(-3,-2).