题目内容
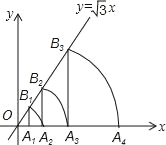
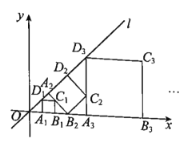
【题目】如图，在平面直角坐标系中，直线l为正比例函数
的图象，点
的坐标为
，过点作x轴的垂线交直线l于点
，以
为边作正方形
；过点
作直线l的垂线，垂足为
，交x轴于点
，以
为边作正方形
；过点
作x轴的垂线，垂足为
，交直线l于点
，以
为边作正方形
；……按此规律操作下去，得到的正方形
的面积是______________．
【答案】
【解析】
根据正比例函数的性质得到
，
，
均为等腰直角三角形，分别求出正方形A1B1C1D1的面积、正方形A2B2C2D2的面积，总结规律解答．
∵点
的坐标为
，
∴点
的坐标为
，
∴正方形
的边长为1，面积为1．
∵直线l为正比例函数
的图象，
∴，，均为等腰直角三角形，
∴
，
，
正方形
的边长为
，面积为
．
同理，正方形
的边长为，面积为
……
所以正方形
的面积是
．
练习册系列答案
相关题目
