题目内容
5.建立一次函数关系解决问题:甲、乙两校为了绿化校园,甲校计划购买A种树苗,A种树苗每棵24元;乙校计划购买B种树苗,B种树苗每棵18元.两校共购买了35棵树苗.若购进B种树苗的数量少于A种树苗的数量,请给出一种两校总费用最少的方案,并求出该方案所需的总费用.分析 甲校购进x棵A种树苗,两校所需要的总费用为w元,根据总费用=购买A树苗所需费用+购买B树苗所需费用,列出函数关系式,根据函数性质确定最值.
解答 解:设甲校购进x棵A种树苗,两校所需要的总费用为w元.
根据题意得:w=24x+18(35-x)=6x+630
∵35-x<x,
∴x>17.5,且x为整数,
在一次函数w=6x+630中,
∵k=6>0,
∴w随x的增大而增大,
∴当x=18时,w有最小值,最小值w=6×18+630=738,
此时35-x=17.
答:甲校购买A种树苗18棵,乙校购买B种树苗17棵,所需的总费用最少,最少为738元.
点评 本题主要考查利用函数性质解决实际问题的能力,建立函数模型是解题关键,利用函数性质确定最值是手段.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
15.下列运算正确的是( )
| A. | 6a-5a=1 | B. | a2+a2=2a4 | C. | 3a2b-4b2a=-a2b | D. | 2a3+3a3=5a3 |
20.已知y是x的一次函数,函数y与自变量x的部分对应值如表,
点(x1,y1),(x2,y2)在该函数的图象上.若x1>x2,则y1<y2.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 10 | 8 | 6 | 4 | 2 | … |
10.三角形的两个内角分别为60°和80°,则它的第三个内角的度数是( )
| A. | 70° | B. | 60° | C. | 50° | D. | 40° |
17. 如图,转盘中四个扇形的面积都相等.小明随意转动转盘2次,当转盘停止转动时,二次指针所指向数字的积为偶数的概率为( )
如图,转盘中四个扇形的面积都相等.小明随意转动转盘2次,当转盘停止转动时,二次指针所指向数字的积为偶数的概率为( )
 如图,转盘中四个扇形的面积都相等.小明随意转动转盘2次,当转盘停止转动时,二次指针所指向数字的积为偶数的概率为( )
如图,转盘中四个扇形的面积都相等.小明随意转动转盘2次,当转盘停止转动时,二次指针所指向数字的积为偶数的概率为( )| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{6}$ |
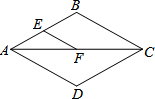 如图,AC是菱形ABCD的对角线,E、F分别是AB、AC的中点,如果EF=2,那么菱形ABCD的周长是16.
如图,AC是菱形ABCD的对角线,E、F分别是AB、AC的中点,如果EF=2,那么菱形ABCD的周长是16. 如图,在△ABC中,∠ACB=90°,D是AB中点,连接CD.若AB=10,则CD的长为( )
如图,在△ABC中,∠ACB=90°,D是AB中点,连接CD.若AB=10,则CD的长为( ) 若有理数a、b、c在数轴上的位置如图所示,则化简:|a|+|a-b|-|c+b|=2a+c.
若有理数a、b、c在数轴上的位置如图所示,则化简:|a|+|a-b|-|c+b|=2a+c. 某菜农搭建了一个横截面为抛物线的大棚,尺寸如图,若菜农身高为1.8m,他在不弯腰的情况下,在棚内的横向活动范围是3m.
某菜农搭建了一个横截面为抛物线的大棚,尺寸如图,若菜农身高为1.8m,他在不弯腰的情况下,在棚内的横向活动范围是3m.