题目内容
10. 如图,将四边形ABCD绕原点O旋转180°得四边形A′B′C′D′.
如图,将四边形ABCD绕原点O旋转180°得四边形A′B′C′D′.(1)画出旋转后的四边形A′B′C′D′;
(2)写出A′、B′、C′、D′的坐标;
(3)四边形ABCD和四边形A′B′C′D′组成的图形是轴对称图形吗?若是,请直接写出对称轴的解析式.
分析 (1)利用网格特点和中心对称的性质画出点A、B、C、D的对应点A′、B′、C′、D′,从而可得到四边形A′B′C′D′;
(2)根据各象限内点的坐标特征写出A′、B′、C′、D′的坐标;
(3)根据轴对称图形的定义进行判断.
解答 解:(1)如图,四边形A′B′C′D′为所作;
(2)A′(3,1)、B′(2,-2)、C′(-1,-2)、D′(2,-1);
(3)四边形ABCD和四边形A′B′C′D′组成的图形不是轴对称图形.
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应点与旋转中心的连线段的夹角都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.

练习册系列答案
相关题目
5. 如图,点A,B在数轴上表示的数分别为a,b,下列式子成立的是( )
如图,点A,B在数轴上表示的数分别为a,b,下列式子成立的是( )
 如图,点A,B在数轴上表示的数分别为a,b,下列式子成立的是( )
如图,点A,B在数轴上表示的数分别为a,b,下列式子成立的是( )| A. | a+b>0 | B. | a-b>0 | C. | ab>0 | D. | a3>0 |
20.等腰三角形一腰上的高与底边的夹角为40°,则顶角的度数为( )
| A. | 40° | B. | 80° | C. | 100° | D. | 80°或100° |
 如图,把长方形ABCD沿EF对折,若∠1=52°,则∠AEF的度数等于116°.
如图,把长方形ABCD沿EF对折,若∠1=52°,则∠AEF的度数等于116°.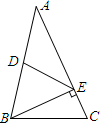 如图,△ABC中,E在AC上,且BE⊥AC.D为AB中点,若DE=5,AE=8,则BE的长为6.
如图,△ABC中,E在AC上,且BE⊥AC.D为AB中点,若DE=5,AE=8,则BE的长为6.