题目内容
抛物线y=-x2+2x+3与x轴交于A,B两点,与y轴交于C,抛物线的顶点为M
(1)△ABC的面积= ,△ABM的面积= .
(2)利用图象可得,当x满足 时,0≤y≤3.
(1)△ABC的面积=
(2)利用图象可得,当x满足
考点:抛物线与x轴的交点
专题:
分析:(1)根据函数解析式求得A、B、C、M点的坐标,然后由三角形的面积公式进行计算;
(2)根据图示直接填空.
(2)根据图示直接填空.
解答: 解:(1)∵在y=-x2+2x+3中,当x=0时,y=3,
解:(1)∵在y=-x2+2x+3中,当x=0时,y=3,
∴C(0,3),
又y=-x2+2x+3=-(x-3)(x+1),或y=-x2+2x+3=-(x-1)2+4,
∴A(-1,0),B(3,0),M(1,4),
∴AB=4,OC=3,MD=4,
则S△ABC=
AB•OC=
×4×3=6;S△ABM=
AB•MD=
×4×4=8.
故答案是:6;8;
(2)根据图示知,当-1≤x≤0或2≤x≤3时,0≤y≤3.
故答案是:-1≤x≤0或2≤x≤3.
 解:(1)∵在y=-x2+2x+3中,当x=0时,y=3,
解:(1)∵在y=-x2+2x+3中,当x=0时,y=3,∴C(0,3),
又y=-x2+2x+3=-(x-3)(x+1),或y=-x2+2x+3=-(x-1)2+4,
∴A(-1,0),B(3,0),M(1,4),
∴AB=4,OC=3,MD=4,
则S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案是:6;8;
(2)根据图示知,当-1≤x≤0或2≤x≤3时,0≤y≤3.
故答案是:-1≤x≤0或2≤x≤3.
点评:本题考查了抛物线与x轴的交点.此题利用抛物线的对称性求得x的取值范围.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
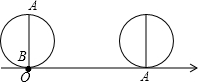 王老师在讲“实数”这节时,做了如下实验:如图所示,AB是半径为1的圆的直径,将B点放在数轴的原点上,将圆沿数轴向右滚动,A点刚好落在数轴上时,A点对应的数为
王老师在讲“实数”这节时,做了如下实验:如图所示,AB是半径为1的圆的直径,将B点放在数轴的原点上,将圆沿数轴向右滚动,A点刚好落在数轴上时,A点对应的数为