题目内容
15.若实数x、z满足$\sqrt{x-6}+{(x-z+4)^2}$=0,且实数y的立方根是2.(1)分别求x、y、z的值;
(2)若x、y、z是△ABC的三边长,试判断△ABC的形状.
分析 (1)根据非负数的性质和立方根的定义解答即可;
(2)根据勾股定理的逆定理进行判断即可.
解答 解:(1)由题意得,x-6=0,x-z+4=0,$\root{3}{y}$=2,
解得,x=6,z=10,y=8,;
(2)∵x2+y2=100,z2=100,
∴x2+y2=z2,
∴△ABC是直角三角形.
点评 本题考查的是非负数的性质和勾股定理的逆定理,掌握几个非负数的和为0时,这几个非负数都为0是解题的关键.

练习册系列答案
相关题目
4. 如图,数轴上点A所表示的数可能是( )
如图,数轴上点A所表示的数可能是( )
 如图,数轴上点A所表示的数可能是( )
如图,数轴上点A所表示的数可能是( )| A. | 2.5 | B. | -1.5 | C. | -2.4 | D. | 1.5 |
5.种一批树,如果每人种10棵,则剩6棵未种;如果每人种12棵,则缺6棵,设有x棵树,则根据题意列出方程正确的是( )
| A. | 10x-6=12x+6 | B. | $\frac{x-6}{10}$=$\frac{x+6}{12}$ | C. | 10x+6=12x-6 | D. | $\frac{x+6}{10}$=$\frac{x-6}{12}$ |
 小韵从如图的二次函数y=ax2+bx+c图象中,观察的处理下面四条信息:
小韵从如图的二次函数y=ax2+bx+c图象中,观察的处理下面四条信息: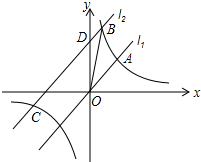 如图,直线l1:y=x与双曲线y=$\frac{k}{x}$相交于点A(3,a),将直线l1沿y轴向上平移8个单位单位得到l2,直线l2与双曲线相交于B、C两点(点B在第一象限),交y轴于D点.
如图,直线l1:y=x与双曲线y=$\frac{k}{x}$相交于点A(3,a),将直线l1沿y轴向上平移8个单位单位得到l2,直线l2与双曲线相交于B、C两点(点B在第一象限),交y轴于D点.