题目内容
16．
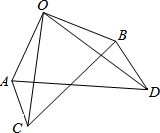已知：如图，△AOC≌△BOD．求证：△AOD≌△BOC．
分析 先根据全等三角形的性质由△AOC≌△BOD得到OA=OB，OC=OD，∠AOC=∠BOD，则∠AOD=∠BOC，然后根据“SAS”可判断△AOD≌△BOC．
解答 证明：∵△AOC≌△BOD，
∴OA=OB，OC=OD，∠AOC=∠BOD，
∴∠AOC+∠COD=∠BOD+∠COD，即∠AOD=∠BOC，
在△AOD和△BOC中，
$\left\{\begin{array}{l}{AO=BO}\\{∠AOD=∠BOC}\\{OD=OC}\end{array}\right.$，
∴△AOD≌△BOC．
点评 本题考查了全等三角形的判定：全等三角形的5种判定方法中，选用哪一种方法，取决于题目中的已知条件，若已知两边对应相等，则找它们的夹角或第三边．
练习册系列答案
长江作业本同步练习册系列答案
相关题目
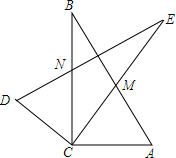两个形状大小完全一样的两个Rt△ACB和Rt△DCE如图放置，设两直角边BC、CE的夹角∠ECB=α，∠A=β．
如图，锐角△ABC的外接圆O．在BC边上取两点D、E使∠BAD=∠CAE，EM⊥AB于点M，EN⊥AC于点N，AD的延长线交⊙O于点P．求证：AP•MN=AB•AC•sin∠BAC．
11．一次考试中，某题的得分情况如下表所示，则x等于30%．
| 得分（分） | 0 | 1 | 2 | 3 | 4 |
| 百分率 | 10% | 25% | x | 30% | 5% |
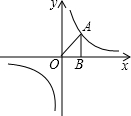如图所示，A为反比例函数$y=\frac{k}{x}$图象上一点，AB垂直x轴，垂足为B点，若S△AOB=3，则k的值为6．
8．若抛物线y=x2+（m-1）x+（m+3）的顶点在坐标轴上，则m的值有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
