ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ≈ΉΈοœΏ![]() ΘΚ
ΘΚ![]() ”κ
”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() ΓΔ
ΓΔ![]() ΝΫΒψΘ§”κ
ΝΫΒψΘ§”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() Θ§«“
Θ§«“![]() Θ°
Θ°
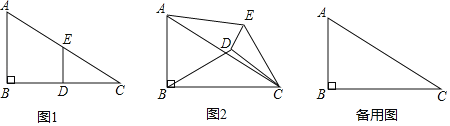
Θ®1Θ©÷±Ϋ”–¥≥ω≈ΉΈοœΏ![]() ΒΡΫβΈω ΫΘΜ
ΒΡΫβΈω ΫΘΜ
Θ®2Θ©»γΆΦ1Θ§Βψ![]() ‘Ύ
‘Ύ![]() ÷αΉσ≤ύΒΡ≈ΉΈοœΏ
÷αΉσ≤ύΒΡ≈ΉΈοœΏ![]() …œΘ§ΫΪΒψ
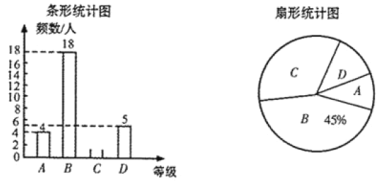
…œΘ§ΫΪΒψ![]() œ»œρ”“ΤΫ“Τ4ΗωΒΞΈΜ≥ΛΕ»Θ§‘Όœρœ¬ΤΫ“Τ
œ»œρ”“ΤΫ“Τ4ΗωΒΞΈΜ≥ΛΕ»Θ§‘Όœρœ¬ΤΫ“Τ![]() ΗωΒΞΈΜ≥ΛΕ»Θ§ΒΟΒΫΒΡΕ‘”ΠΒψ
ΗωΒΞΈΜ≥ΛΕ»Θ§ΒΟΒΫΒΡΕ‘”ΠΒψ![]() «ΓΚΟ¬δ‘Ύ≈ΉΈοœΏ
«ΓΚΟ¬δ‘Ύ≈ΉΈοœΏ![]() …œΘ§»τ
…œΘ§»τ![]() Θ§«σΒψ
Θ§«σΒψ![]() ΒΡΉχ±ξΘΜ
ΒΡΉχ±ξΘΜ
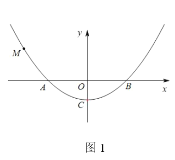
Θ®3Θ©»γΆΦ2Θ§ΫΪ≈ΉΈοœΏ![]() œρ…œΤΫ“Τ2ΗωΒΞΈΜ≥ΛΕ»ΒΟΒΫ≈ΉΈοœΏ
œρ…œΤΫ“Τ2ΗωΒΞΈΜ≥ΛΕ»ΒΟΒΫ≈ΉΈοœΏ![]() Θ§“Μ¥ΈΚ· ΐ
Θ§“Μ¥ΈΚ· ΐ![]() ΒΡΆΦœσ
ΒΡΆΦœσ![]() ”κ≈ΉΈοœΏ
”κ≈ΉΈοœΏ![]() ÷Μ”–“ΜΗωΙΪΙ≤Βψ
÷Μ”–“ΜΗωΙΪΙ≤Βψ![]() Θ§”κ
Θ§”κ![]() ÷αΫΜ”ΎΒψ
÷αΫΜ”ΎΒψ![]() Θ§ΧΫΨΩΘΚ
Θ§ΧΫΨΩΘΚ![]() ÷α…œ «Ζώ¥φ‘ΎΕ®Βψ
÷α…œ «Ζώ¥φ‘ΎΕ®Βψ![]() ¬ζΉψ
¬ζΉψ![]() ΘΩ»τ¥φ‘ΎΘ§«σ≥ωΒψ
ΘΩ»τ¥φ‘ΎΘ§«σ≥ωΒψ![]() ΒΡΉχ±ξΘΜΖώ‘ρΘ§ΥΒΟςάμ”…Θ°
ΒΡΉχ±ξΘΜΖώ‘ρΘ§ΥΒΟςάμ”…Θ°
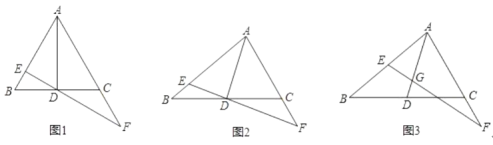
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©
ΘΜΘ®2Θ©![]() Μρ
Μρ![]() ΘΜΘ®3Θ©¥φ‘ΎΘ§
ΘΜΘ®3Θ©¥φ‘ΎΘ§![]()
ΓΨΫβΈωΓΩ
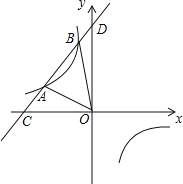
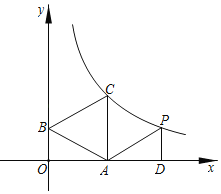
Θ®1Θ©ΗυΨίΧβ“βΘ§«σ≥ωΒψBΒΡΉχ±ξΘ§»ΜΚσΫΪΒψBΓΔCΒΡΉχ±ξ¥ζ»κ≈ΉΈοœΏΒΡΫβΈω Ϋ÷–Φ¥Ω…«σ≥ωΫα¬έΘΜ
Θ®2Θ©…η![]() Θ§‘ρ
Θ§‘ρ![]() Θ§άϊ”Ο¥ΐΕ®œΒ ΐΖ®«σ≥ω÷±œΏMCΒΡΫβΈω ΫΘ§ΙΐΒψ
Θ§άϊ”Ο¥ΐΕ®œΒ ΐΖ®«σ≥ω÷±œΏMCΒΡΫβΈω ΫΘ§ΙΐΒψ![]() Ής
Ής![]() ÷αΫΜ
÷αΫΜ![]() ”Ύ
”Ύ![]() Θ§ΗυΨίΒψN”κy÷αΒΡΈΜ÷ΟΙΊœΒΖ÷άύΧ÷¬έΘ§άϊ”ΟΓΑ«Π¥ΙΗΏΘ§Υ°ΤΫΩμΓ±Ν–≥ωΖΫ≥ΧΘ§Φ¥Ω…«σ≥ωΫα¬έΘΜ
Θ§ΗυΨίΒψN”κy÷αΒΡΈΜ÷ΟΙΊœΒΖ÷άύΧ÷¬έΘ§άϊ”ΟΓΑ«Π¥ΙΗΏΘ§Υ°ΤΫΩμΓ±Ν–≥ωΖΫ≥ΧΘ§Φ¥Ω…«σ≥ωΫα¬έΘΜ
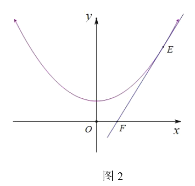
Θ®3Θ©ΗυΨίΧβ“βΩ…ΒΟΤΫ“ΤΚσΒΡΕΰ¥ΈΚ· ΐΫβΈω ΫΈΣ![]() Θ§…η
Θ§…η![]() Θ§«σ≥ω÷±œΏlΒΡΫβΈω ΫΘ§»ΜΚσΝΣΝΔΖΫ≥ΧΘ§ΝνΓς=0Φ¥Ω…«σ≥ω
Θ§«σ≥ω÷±œΏlΒΡΫβΈω ΫΘ§»ΜΚσΝΣΝΔΖΫ≥ΧΘ§ΝνΓς=0Φ¥Ω…«σ≥ω![]() Θ§ΙΐΒψ
Θ§ΙΐΒψ![]() Ής
Ής![]() ”Ύ
”Ύ![]() Θ§Φ«Ε®Βψ
Θ§Φ«Ε®Βψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() ΓΔ
ΓΔ![]() Θ§άϊ”ΟœύΥΤ»ΐΫ«–ΈΒΡ≈–Ε®÷Λ≥ω
Θ§άϊ”ΟœύΥΤ»ΐΫ«–ΈΒΡ≈–Ε®÷Λ≥ω![]() Θ§Ν–≥ω±»άΐ ΫΦ¥Ω…«σ≥ωΫα¬έΘ°
Θ§Ν–≥ω±»άΐ ΫΦ¥Ω…«σ≥ωΫα¬έΘ°
ΫβΘΚΘ®1Θ©ΓΏ![]()
ΓύOC=1
ΓΏAB=4OC
ΓύAB=4
ΓΏ≈ΉΈοœΏΒΡΕ‘≥Τ÷αΈΣy÷α
ΓύOB=2
ΓύΒψBΒΡΉχ±ξΈΣΘ®2,0Θ©
ΫΪΒψBΓΔCΒΡΉχ±ξ¥ζ»κ![]() ÷–Θ§ΒΟ
÷–Θ§ΒΟ
![]()
Γύ≈ΉΈοœΏ![]() ΒΡΫβΈω ΫΈΣ
ΒΡΫβΈω ΫΈΣ![]() Θ°
Θ°
Θ®2Θ©ΫβΘΚΩ……η![]() Θ§‘ρ
Θ§‘ρ![]() Θ§
Θ§
![]() Θ§
Θ§
![]() …η
…η![]() Θ§
Θ§
ΫΪΒψNΒΡΉχ±ξ¥ζ»κΘ§ΒΟ
Ω…ΒΟΘΚ![]() Θ§
Θ§
ΙΐΒψ![]() Ής
Ής![]() ÷αΫΜ
÷αΫΜ![]() ”Ύ
”Ύ![]() Θ§
Θ§
![]() Θ§
Θ§
«ιΩω“ΜΘΚΒ±Βψ![]() ‘Ύ
‘Ύ![]() ÷αΉσ≤ύ ±Θ§‘ρ
÷αΉσ≤ύ ±Θ§‘ρ![]()
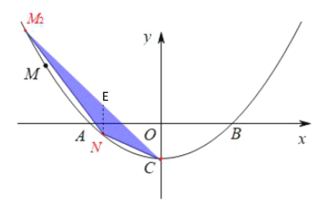
Γύ![]()
![]()
ΫβΒΟΘ§![]() Θ§
Θ§![]() Θ®…α»ΞΘ©Θ§
Θ®…α»ΞΘ©Θ§
Γύ¥Υ ±M![]()
«ιΩωΕΰΘΚΒ±Βψ![]() ‘Ύ
‘Ύ![]() ÷α”“≤ύ ±Θ§‘ρ
÷α”“≤ύ ±Θ§‘ρ![]()
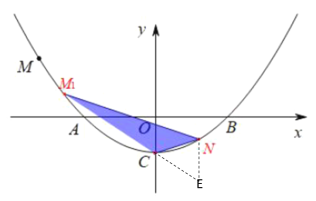
Γύ![]()
![]()
ΫβΒΟΘ§![]()
Γύ¥Υ ±![]()
Ήέ…œΘΚ![]() Μρ
Μρ![]() Θ°
Θ°
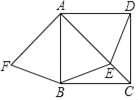
Θ®3Θ©ΫβΘΚ¥φ‘ΎΘ§
”…Χβ“βΩ…÷ΣΘΚΤΫ“ΤΚσΒΡΕΰ¥ΈΚ· ΐΫβΈω ΫΈΣ![]()
“άΧβ“βΩ……η![]() Θ§
Θ§
ΫΪ![]() ¥ζ»κl÷–Θ§
¥ζ»κl÷–Θ§
Ω…ΒΟ![]() ΘΚ
ΘΚ![]()
ΝΣΝΔ
’ϊάμΒΟΘ§![]()
![]()
![]()
Φ¥![]() ΘΚ
ΘΚ![]()
Β±![]() ±Θ§‘ρ
±Θ§‘ρ![]()
![]()
ΙΐΒψ![]() Ής
Ής![]() ”Ύ
”Ύ![]() Θ§Φ«Ε®Βψ
Θ§Φ«Ε®Βψ![]() Θ§Ν§Ϋ”
Θ§Ν§Ϋ”![]() ΓΔ
ΓΔ![]() Θ§
Θ§
![]() Θ§
Θ§
![]() Θ§
Θ§
ΓύΓœHEGΘΪΓœEGH=90ΓψΘ§ΓœOGFΘΪΓœEGH=90Γψ
ΓύΓœHEG=ΓœOGF
![]() Θ§
Θ§
![]()
 Θ§
Θ§
ΫβΒΟΘ§![]() Μρ
Μρ![]() Θ®”…GΈΣΕ®ΒψΘ§Ι …α»ΞΘ©
Θ®”…GΈΣΕ®ΒψΘ§Ι …α»ΞΘ©
![]() Θ°
Θ°


 ΫΧ≤Ρ»ΪΫβΉ÷¥ ΨδΤΣœΒΝ–¥πΑΗ
ΫΧ≤Ρ»ΪΫβΉ÷¥ ΨδΤΣœΒΝ–¥πΑΗ