题目内容
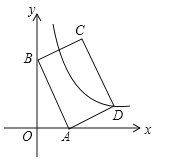
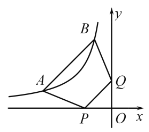
【题目】如图,一次函数y=﹣![]() x+2的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限作等边△ABC.
x+2的图象与x轴、y轴分别交于点A、B,以线段AB为边在第一象限作等边△ABC.
(1)若点C在反比例函数y=![]() 的图象上,求该反比例函数的解析式;
的图象上,求该反比例函数的解析式;
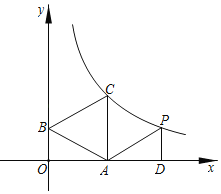
(2)点P(4![]() ,m)在第一象限,过点P作x轴的垂线,垂足为D,当△PAD与△OAB相似且P点在(1)中反比例函数图象上时,求出P点坐标.
,m)在第一象限,过点P作x轴的垂线,垂足为D,当△PAD与△OAB相似且P点在(1)中反比例函数图象上时,求出P点坐标.
【答案】(1)y=![]() ;(2)P点坐标为(4
;(2)P点坐标为(4![]() ,2).
,2).
【解析】
(1)根据坐标轴上点的坐标特征分别求出点![]() 、
、![]() 的坐标,根据正切的定义求出
的坐标,根据正切的定义求出![]() ,根据等边三角形的性质求出点
,根据等边三角形的性质求出点![]() 的坐标,利用待定系数法求出反比例函数的解析式;
的坐标,利用待定系数法求出反比例函数的解析式;
(2)分![]() 、
、![]() 两种情况,根据相似三角形的性质分别求出点
两种情况,根据相似三角形的性质分别求出点![]() 的坐标,代入反比例函数解析式,判断即可.
的坐标,代入反比例函数解析式,判断即可.
解:(1)对于一次函数![]() ,
,
当![]() ,即
,即![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
则点![]() 的坐标为
的坐标为![]() ,
,![]() ,点
,点![]() 的坐标为
的坐标为![]() ,即
,即![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 为等边三角形,
为等边三角形,
![]() ,
,![]() ,
,
![]() ,
,
![]() 点
点![]() 的坐标为:
的坐标为:![]() ,
,![]() ,
,
![]() ,
,
![]() 反比例函数的解析式为:
反比例函数的解析式为:![]() ;
;
(2)![]() 点
点![]() ,
,![]() 在第一象限,
在第一象限,
![]() ,
,![]() ,
,
![]() ,
,
当![]() 时,
时,![]() ,即
,即![]() ,
,
解得,![]() ,此时
,此时![]() 点坐标为
点坐标为![]() ,
,![]() ;
;
当![]() 时,
时,![]() ,即
,即![]() ,
,
解得,![]() ,此时
,此时![]() 点坐标为
点坐标为![]() ,
,![]() ;
;
![]() ,
,![]() ,
,
![]() 点在(1)中反比例函数图象上时,
点在(1)中反比例函数图象上时,![]() 点坐标为
点坐标为![]() ,
,![]() .
.

【题目】为弘扬传统文化,某校开展了“传承经典文化,阅读经典名著”活动.为了解七、八年级学生(七、八年级各有600名学生)的阅读效果,该校举行了经典文化知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
收集数据:
七年级:79,85,73,80,75,76,87,70,75,94,75,79,81,71,75,80,86,59,83,77.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理数据:
|
|
|
|
|
| |
七年级 | 0 | 1 | 0 | a | 7 | 1 |
八年级 | 1 | 0 | 0 | 7 | b | 2 |
分析数据:
平均数 | 众数 | 中位数 | |
七年级 | 78 | 75 |
|
八年级 | 78 |
| 80.5 |
应用数据:
(1)由上表填空:a= ,b= ,c= ,d= .
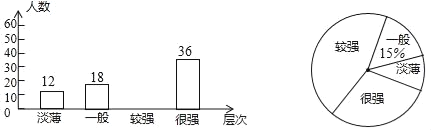
(2)估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人?
(3)你认为哪个年级的学生对经典文化知识掌握的总体水平较好,请说明理由.
【题目】为保障我国海外维和部队官兵的生活,现需通过A港口、B港口分别运送100吨和50吨生活物资.已知该物资在甲仓库存有80吨,乙仓库存有70吨,若从甲、乙两仓库运送物资到港口A的费用分别为14元/吨,20元/吨;从甲、乙两仓库运送物资到港口B的费用分别为10元/吨、8元/吨.
(Ⅰ)设从甲仓库运往A港口x吨,试填写表格.
表一
港口 | 从甲仓库运(吨) | 从乙仓库运(吨) |
A港 |
|
|
B港 |
|
|
表二
港口 | 从甲仓库运到港口费用(元) | 从乙仓库运到港口费用(元) |
A港 | 14x |
|
B港 |
|
|
(Ⅱ)给出能完成此次运输任务的最节省费用的调配方案,并说明理由.