题目内容
2. 如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD,下列结论错误的是( )
如图,在△ABC中,∠A=36°,AB=AC,AB的垂直平分线OD交AB于点O,交AC于点D,连接BD,下列结论错误的是( )| A. | ∠C=2∠A | B. | BD平分∠ABC | C. | S△BCD=S△BOD | D. | BD=BC |
分析 求出∠C的度数即可判断A;求出∠ABC和∠ABD的度数,求出∠DBC的度数,即可判断B;根据三角形面积即可判断C;继而证得△BCD是等腰三角形,则可判断D.
解答 解:A、∵∠A=36°,AB=AC,
∴∠C=∠ABC=72°,
∴∠C=2∠A,正确,
B、∵DO是AB垂直平分线,
∴AD=BD,
∴∠A=∠ABD=36°,
∴∠DBC=72°-36°=36°=∠ABD,
∴BD是∠ABC的角平分线,正确,
C,根据已知不能推出△BCD的面积和△BOD面积相等,错误,
D,∵∠ABD=36°,∠C=72°,
∴∠BDC=72°,
∴∠BDC=∠BCD,
∴BD=BC,正确.
故选C.
点评 本题考查了等腰三角形性质,线段垂直平分线性质的应用,主要考查学生的推理能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12. 如图,△ABC≌△DEF,则图中相等的线段有( )对.
如图,△ABC≌△DEF,则图中相等的线段有( )对.
 如图,△ABC≌△DEF,则图中相等的线段有( )对.
如图,△ABC≌△DEF,则图中相等的线段有( )对.| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
13.2<x<3,化简$\sqrt{{{(x-2)}^2}}$+|3-x|的正确结果是( )
| A. | 1 | B. | -1 | C. | 2x-5 | D. | 5-2x |
10.计算(5+2$\sqrt{6}$)10•(2$\sqrt{6}$-5)20的值为( )
| A. | -1 | B. | 1 | C. | 13 | D. | 169 |
17.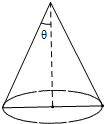 已知圆锥的底面半径为5cm,侧面积为60πcm2,设圆锥的母线与高的夹角为θ,则sinθ的值为( )
已知圆锥的底面半径为5cm,侧面积为60πcm2,设圆锥的母线与高的夹角为θ,则sinθ的值为( )
 已知圆锥的底面半径为5cm,侧面积为60πcm2,设圆锥的母线与高的夹角为θ,则sinθ的值为( )
已知圆锥的底面半径为5cm,侧面积为60πcm2,设圆锥的母线与高的夹角为θ,则sinθ的值为( )| A. | $\frac{3}{13}$ | B. | $\frac{5}{13}$ | C. | $\frac{5}{12}$ | D. | $\frac{12}{13}$ |
7.若k<0,b<0,则一次函数y=kx+b的图象经过( )
| A. | 第一、二、四象限 | B. | 第一、三、四象限 | C. | 第二、三、四象限 | D. | 第一、三、四象限 |
14.某批发店将进价为4元的小商品按5元卖出时,可卖出500件,已知这种商品每件涨价1元,其销售量就减少10件,若要赚得5600元利润,售价应定为( )
| A. | 20元 | B. | 39元 | C. | 20元或39元 | D. | 50元 |
11.有5名同学参加演讲比赛,以抽签的方式决定每个人的出场顺序,签筒中有5根形状大小相同的纸签,上面分别标有出场的序号1,2,3,4,5.小军首先抽签,他在看不到纸签上的数字的情况下从签筒中随机地抽取一根纸签,下列事件是随机事件的是( )
| A. | 抽取一根纸签,抽到的序号是0 | |
| B. | 抽取一根纸签,抽到的序号小于6 | |
| C. | 抽取一根纸签,抽到的序号是1 | |
| D. | 抽取一根纸签,抽到的序号有6种可能的结果 |
12.下列各式中,一定为二次根式的是( )
| A. | $\sqrt{-5}$ | B. | $\root{3}{m}$ | C. | $\sqrt{2m}$ | D. | $\sqrt{{m}^{2}+1}$ |