��Ŀ����
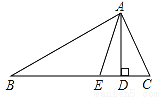
��֪����ͼ���ڡ�ABC�У�AD��AE�ֱ��ǡ�ABC�ĸߺͽ�ƽ���ߣ�
��1������B=30�㣬��C=50�㣬���DAE�Ķ�����
��2�����ʡ�DAE���C����B��������������ϵ��˵�����ɣ�
��ϰ��ϵ�д�
�����Ŀ
��Ŀ����
��֪����ͼ���ڡ�ABC�У�AD��AE�ֱ��ǡ�ABC�ĸߺͽ�ƽ���ߣ�
��1������B=30�㣬��C=50�㣬���DAE�Ķ�����
��2�����ʡ�DAE���C����B��������������ϵ��˵�����ɣ�
