��Ŀ����
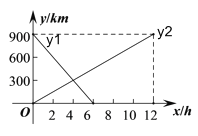
����Ŀ��һ�п쳵�Ӽ�ʻ���ҵأ�һ���������ҵ�ʻ���أ�����ͬʱ��������������ʻ��ʱ��Ϊx(h)������֮��ľ���Ϊy(km)��ͼ�е����߱�ʾy��x֮��ĺ�����ϵ��
����ͼ���������̽����
�����ʼ������ص�·��Ϊ ��
���������Ϳ쳵���ٶȣ�
�����߶�BC����ʾ��y��x֮��ĺ�����ϵʽ����д���Ա���x��ȡֵ��Χ��
�������������ʻ��ʱ��Ϊx(h),�����������ҵصľ���ֱ�Ϊy1(km)��y2(km)��������ͼ�л���y1��y2��x�ĺ���ͼ��


���𰸡���1���������ص�·��Ϊ900km��
��2���������ٶ�Ϊ![]() ���쳵���ٶ�Ϊ150km/h��
���쳵���ٶ�Ϊ150km/h��
��3���߶�![]() ����ʾ��
����ʾ��![]() ��
��![]() ֮��ĺ�����ϵʽΪ
֮��ĺ�����ϵʽΪ![]() ���Ա���
���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��![]() ��
��
��4��������.
��������
��1������ͼ���ֱ�ӵó��𰸣�
��2����ͼ���֪������12h��ʻ��·��Ϊ900km����������ʻ4hʱ�������Ϳ쳵������Ȼ�������ٶȺ�·��֮��Ĺ�ϵ��⼴�ɣ�
��3���ֱ��������ó���C������Ϊ��6��450�����ѣ�4��0������6��450������y��kx��b���ô���ϵ������⣬Ȼ��д���Ա���x��ȡֵ��Χ���ɣ�
��4������쳵���������Ե���Ŀ�ĵ������ʱ�䣬���ɵó�����ͼ���ĵ�����꣬Ȼ��ͼ����.
�⣺��1����ͼ�ɵã��������ص�·��Ϊ900km��
��2����ͼ���֪������12h��ʻ��·��Ϊ900km��
�����������ٶ�Ϊ![]() ��
��
��������ʻ4hʱ�������Ϳ쳵������������ʻ��·��֮��Ϊ900km��
���������Ϳ쳵��ʻ���ٶ�֮��Ϊ![]() ��
��
���Կ쳵���ٶ�Ϊ150km/h��
��3����Ϊ�쳵��ʻ900km�����ҵأ�
���Կ쳵��ʻ![]() �����ҵأ���ʱ����֮��ľ���Ϊ
�����ҵأ���ʱ����֮��ľ���Ϊ![]() ��
��
���Ե�![]() ������Ϊ
������Ϊ![]() ��
��
���߶�![]() ����ʾ��
����ʾ��![]() ��
��![]() ֮��ĺ�����ϵʽΪ
֮��ĺ�����ϵʽΪ![]() ��
��
��![]() ��
��![]() �����
�����![]() �����
�����![]() ��
��
�����߶�![]() ����ʾ��
����ʾ��![]() ��
��![]() ֮��ĺ�����ϵʽΪ
֮��ĺ�����ϵʽΪ![]() ���Ա���
���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��![]() ��
��
��4��������ã�y1���㣨0��900����y2���㣨0��0����
�쳵���ҵص�ʱ��Ϊ��![]() ���������ص�ʱ��Ϊ��
���������ص�ʱ��Ϊ��![]() ��
��
��y1���㣨6��0����y2���㣨12��900����
��ͼ��ʾ��