题目内容
14.下列关于x的方程(k-1)x2+2kx+2=0根的情况说法正确的是( )| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 没有实数根 | D. | 总有实数根 |
分析 当k-1=0时,可通过解一元一次方程,找出方程的解;当k-1≠0时,根据方程的系数结合根的判别式,即可得出△=4(k-1)2≥0,由此可得出该方程有实数根.综上即可得出结论.
解答 解:当k-1=0,即k=1时,原方程为2x+2=0,
解得:x=-1;
当k-1≠0,即k≠1时,△=(2k)2-4×2×(k-1)=4(k-1)2≥0,
∴此时方程有实数根.
综上所述:无论k为何值,关于x的方程(k-1)x2+2kx+2=0总有实数根.
故选D.
点评 本题考查了解一元一次方程以及根的判别式,分k-1=0与k-1≠0两种情况考虑方程解的情况是解题的关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案
相关题目
4. 如图,a∥b,∠1=150°,则∠2等于( )
如图,a∥b,∠1=150°,则∠2等于( )
 如图,a∥b,∠1=150°,则∠2等于( )
如图,a∥b,∠1=150°,则∠2等于( )| A. | 30° | B. | 90° | C. | 60° | D. | 50° |
19.一个菱形的四个内角度数之比依次为1:2:3:4,这个事件是( )
| A. | 必然事件 | B. | 随机事件 | C. | 不可能事件 | D. | 以上都不是 |
6. 如图,直线l1∥l2,若∠1=70°,∠2=60°,则∠3的度数为( )
如图,直线l1∥l2,若∠1=70°,∠2=60°,则∠3的度数为( )
 如图,直线l1∥l2,若∠1=70°,∠2=60°,则∠3的度数为( )
如图,直线l1∥l2,若∠1=70°,∠2=60°,则∠3的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
3.已知正方体的体积为2$\sqrt{2}$,则这个正方体的棱长为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{6}$ | D. | 3 |
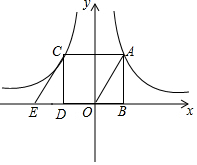 在平面直角坐标系中,把图中的Rt△ABO(∠ABO=90°)沿x轴负半轴平移得到△CDE,已知OB=3,AB=4,函数y1=$\frac{{k}_{1}}{x}$(x>0)的图象经过点A.
在平面直角坐标系中,把图中的Rt△ABO(∠ABO=90°)沿x轴负半轴平移得到△CDE,已知OB=3,AB=4,函数y1=$\frac{{k}_{1}}{x}$(x>0)的图象经过点A.
 小明对九(1)班同学“你最喜欢的球类项目是什么?(只选一项)”的问题进行了调查,把所得数据绘制成如图所示的扇形统计图.由图可知,该班同学最喜欢的球类项目是( )
小明对九(1)班同学“你最喜欢的球类项目是什么?(只选一项)”的问题进行了调查,把所得数据绘制成如图所示的扇形统计图.由图可知,该班同学最喜欢的球类项目是( )