题目内容
弦AB、CD交于点P,P是AB的中点,PC=2,PD=8,则AB等于
- A.9
- B.8
- C.7
- D.6
B
分析:根据题意画出图形,直接根据相交弦定理即可得出结论.
解答: 解:如图所示:
解:如图所示:
∵P是AB的中点,PC=2,PD=8,
∴AP2=PC•PD,即AP2=2×8=16,
∴AP=4,
∴AB=2AP=8.
故选B.
点评:本题考查的是相交弦定理,根据题意画出图形,利用数形结合求解是解答此题的关键.
分析:根据题意画出图形,直接根据相交弦定理即可得出结论.
解答:
 解:如图所示:
解:如图所示:∵P是AB的中点,PC=2,PD=8,
∴AP2=PC•PD,即AP2=2×8=16,
∴AP=4,
∴AB=2AP=8.
故选B.
点评:本题考查的是相交弦定理,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知,如图
已知,如图 |
| BC |
 |
| AD |
| A、120° | B、100° |
| C、80° | D、60° |
 8、如图,已知⊙O的弦AB,CD交于点P,且OP⊥CD,若CD=4,则AP•BP的值为( )
8、如图,已知⊙O的弦AB,CD交于点P,且OP⊥CD,若CD=4,则AP•BP的值为( ) 2、⊙O的两条弦AB,CD交于点P,已知AP=4,BP=6,CP=3,求CD的长.
2、⊙O的两条弦AB,CD交于点P,已知AP=4,BP=6,CP=3,求CD的长.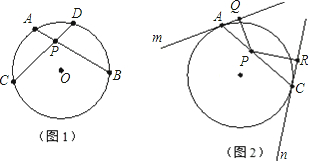
 已知:如图,在⊙O中,弦AB、CD交于点E,AD=CB.求证:AE=CE.
已知:如图,在⊙O中,弦AB、CD交于点E,AD=CB.求证:AE=CE.