题目内容
 如图,∠A=36°,∠C=72°,BE为∠ABC的平分线,DE∥BC,则图中等腰三角形的个数有
如图,∠A=36°,∠C=72°,BE为∠ABC的平分线,DE∥BC,则图中等腰三角形的个数有
- A.6个
- B.5个
- C.4个
- D.3个
C
分析:根据三角形内角和定理判定△ABC为等腰三角形,然后由角平分线、平行线的性质、等角对等边来找图中的等腰三角形.
解答: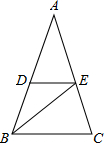 解:∵在△ABC中,∠A=36°,∠C=72°,
解:∵在△ABC中,∠A=36°,∠C=72°,
∴∠ABC=72°,
①∴∠ABC=∠C,
∴AB=AC,
∴△ABC是等腰三角形;
②∵AB=AC,DE∥BC,
∴AD=AE,
∴△ADE是等腰三角形;
③∵BE为∠ABC的平分线,
∴∠ABE= ∠ABC=36°,
∠ABC=36°,
∴∠A=∠ABE=36°,
∴AE=BE,
∴△ABE为等腰三角形;
④∵∠ABC=72°,BE为∠ABC的平分线,DE∥BC,
∠EBC=∠EBD=∠DEB=36°,
∴DB=DE,
∴△DBE是等腰三角形;
综上所述,图中的等腰三角形有4个;
故选C.
点评:本题考查了等腰三角形的判定.角的等量代换的运用是正确解答本题的关键.
分析:根据三角形内角和定理判定△ABC为等腰三角形,然后由角平分线、平行线的性质、等角对等边来找图中的等腰三角形.
解答:
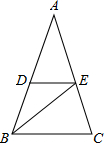 解:∵在△ABC中,∠A=36°,∠C=72°,
解:∵在△ABC中,∠A=36°,∠C=72°,∴∠ABC=72°,
①∴∠ABC=∠C,
∴AB=AC,
∴△ABC是等腰三角形;
②∵AB=AC,DE∥BC,
∴AD=AE,
∴△ADE是等腰三角形;
③∵BE为∠ABC的平分线,
∴∠ABE=
 ∠ABC=36°,
∠ABC=36°,∴∠A=∠ABE=36°,
∴AE=BE,
∴△ABE为等腰三角形;
④∵∠ABC=72°,BE为∠ABC的平分线,DE∥BC,
∠EBC=∠EBD=∠DEB=36°,
∴DB=DE,
∴△DBE是等腰三角形;
综上所述,图中的等腰三角形有4个;
故选C.
点评:本题考查了等腰三角形的判定.角的等量代换的运用是正确解答本题的关键.

练习册系列答案
相关题目
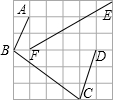 如图是由36个边长为1的小正方形拼成的,连接小正方形中的点A、B、C、D、E、F得线段AB、BC、CD、EF,这些线段中长度是有理数的是哪些?长度是无理数的是哪些?说明理由.
如图是由36个边长为1的小正方形拼成的,连接小正方形中的点A、B、C、D、E、F得线段AB、BC、CD、EF,这些线段中长度是有理数的是哪些?长度是无理数的是哪些?说明理由. 24、如图,∠A=36°,∠DBC=36°,∠C=72°,找出图中的一个等腰三角形,并说明理由.
24、如图,∠A=36°,∠DBC=36°,∠C=72°,找出图中的一个等腰三角形,并说明理由. 20、如图,∠A=36°,∠DBC=36°,∠C=72°,那么,∠1=
20、如图,∠A=36°,∠DBC=36°,∠C=72°,那么,∠1=
 (2013•淄博)在△ABC中,P是AB上的动点(P异于A,B),过点P的一条直线截△ABC,使截得的三角形与△ABC相似,我们不妨称这种直线为过点P的△ABC的相似线.如图,∠A=36°,AB=AC,当点P在AC的垂直平分线上时,过点P的△ABC的相似线最多有
(2013•淄博)在△ABC中,P是AB上的动点(P异于A,B),过点P的一条直线截△ABC,使截得的三角形与△ABC相似,我们不妨称这种直线为过点P的△ABC的相似线.如图,∠A=36°,AB=AC,当点P在AC的垂直平分线上时,过点P的△ABC的相似线最多有