Question

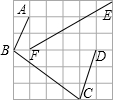
20、如图，∠A=36°，∠DBC=36°，∠C=72°，那么，∠1=

72

°，∠2=

36

°；并且指出图中等腰三角形有

3

个；分别是

△BDC，△ABD，△ABC

．

Answer 1

分析：根据三角形内角和等于180°及等腰三角形的判定，分别求出各个角的度数，再判断是否是等腰三角形解答即可．

解答：解：∵在△ABC中，∠A+∠C+∠DBC+∠2=180°，∠A=36°，∠DBC=36°，∠C=72°，
∴∠2=180°-72°-36°-36°=36°，
∴∠A=∠2=36°，
∴AD=BD，△ADB为等腰三角形；
∠1=180°-72°-36°=72°，
∴∠C=∠1，
∴BD=BC，△BCD是等腰三角形，∠ABC=∠C=72°，
∴AB=AC，
∴△ABC也为等腰三角形．
故填3，△BDC，△ABD，△ABC．

点评：本题考查了等腰三角形的性质和判定、角的平分线的性质及三角形内角和定理；由已知条件利用相关的性质求得各个角的度数是正确解答本题的关键．