题目内容
11.关于x的一元二次方程x2-(m+3)x+m+1=0(1)求证:无论m为何值,方程总有两个不相等的实数根;
(2)当方程根的判别式等于5时,则m=0或-2.
分析 (1)由根的判别式可得出△=(m+1)2+4>0,由此可证出无论m为何值,方程总有两个不相等的实数根;
(2)令△=m2+2m+5=5,解之即可得出m的值.
解答 (1)证明:△=[-(m+3)]2-4(m+1)=m2+2m+5=(m+1)2+4.
∵(m+1)2≥0,
∴(m+1)2+4>0,即△>0,
∴无论m为何值,方程总有两个不相等的实数根;
(2)解:∵△=m2+2m+5=5,
∴m(m+2)=0,
∴m1=0,m2=-2.
故答案为:0或-2.
点评 本题考查了根的判别式以及,因式分解法解一元二次方程,解题的关键是:(1)牢记“当△>0时,方程有两个不相等的实数根”;(2)令△=5,求出m值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
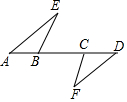 填空:把下面的推理过程补充完整,并在括号内注明理由.
填空:把下面的推理过程补充完整,并在括号内注明理由.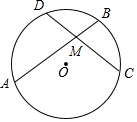 如图,已知圆O,弦AB、CD相交于点M,M为CD中点,且圆O的半径为3,OM=2,求AM•MB的值.
如图,已知圆O,弦AB、CD相交于点M,M为CD中点,且圆O的半径为3,OM=2,求AM•MB的值. 如图,已知l1∥l2∥l3,AB=7,BC=8,DF=18,求EF的长.
如图,已知l1∥l2∥l3,AB=7,BC=8,DF=18,求EF的长.