题目内容
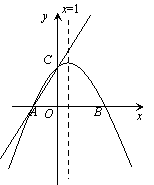
【题目】如图,在平面直角坐标系xOy中,一次函数y=![]() x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.
x+m (m为常数)的图像与x轴交于点A(-3,0),与y轴交于点C.以直线x=1为对称轴的抛物线y=ax2+bx+c(a,b,c为常数,且a≠0)经过A、C两点,并与x轴的正半轴交于点B.
(1)求m的值及抛物线的函数表达式;
(2)若P是抛物线对称轴上一动点,△ACP周长最小时,求出P的坐标;
(3)是否存在抛物在线一动点Q,使得△ACQ是以AC为直角边的直角三角形?若存在,求出点Q的横坐标;若不存在,请说明理由;
(4)在(2)的条件下过点P任意作一条与y轴不平行的直线交抛物线于M1(x1,y1),M2(x2,y2)两点,试问![]() 是否为定值,如果是,请直接写出结果,如果不是请说明理由.
是否为定值,如果是,请直接写出结果,如果不是请说明理由.
【答案】(1)![]() ,y=
,y=![]() x2+
x2+![]() x+
x+![]() ;(2)(1,3);(3)存在,5.2 ,7.2;(4)是.
;(2)(1,3);(3)存在,5.2 ,7.2;(4)是.
【解析】
试题(1)首先求得m的值和直线的解析式,根据抛物线对称性得到B点坐标,根据A、B点坐标利用交点式求得抛物线的解析式;
(2)确定何时△ACP的周长最小.利用轴对称的性质和两点之间线段最短的原理解决;确定P点坐标P(1,3),从而直线M1M2的解析式可以表示为y=kx+3-k;
(3)存在, 设Q(x,-![]() x2+
x2+![]() x+
x+![]() )①若C为直角顶点, 则由△ACO相似于△CQE,得x=5.2,②若A为直角顶点,则由△ACO相似于△AQE,得x=8.2从而求出Q点坐标.
)①若C为直角顶点, 则由△ACO相似于△CQE,得x=5.2,②若A为直角顶点,则由△ACO相似于△AQE,得x=8.2从而求出Q点坐标.
(4)利用两点间的距离公式,分别求得线段M1M2、M1P和M2P的长度,相互比较即可得到结论:![]() 为定值.
为定值.
试题解析:(1)∵y=![]() x+m经过点(-3,0),
x+m经过点(-3,0),
∴0=![]() +m,解得m=
+m,解得m=![]() ,
,
∴直线解析式为y=![]() x+
x+![]() ,C(0,
,C(0,![]() ).
).
∵抛物线y=ax2+bx+c对称轴为x=1,且与x轴交于A(-3,0),∴另一交点为B(5,0),
设抛物线解析式为y=a(x+3)(x-5),
∵抛物线经过C(0,![]() ),
),
∴![]() =a3(-5),解得a=
=a3(-5),解得a=![]() ,
,
∴抛物线解析式为y=![]() x2+
x2+![]() x+
x+![]() ;
;
(2)要使△ACP的周长最小,只需AP+CP最小即可.如图2,
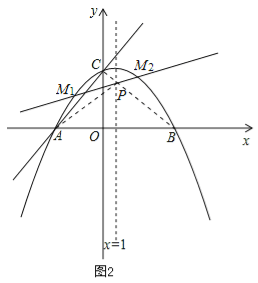
连接BC交x=1于P点,因为点A、B关于x=1对称,根据轴对称性质以及两点之间线段最短,可知此时AP+CP最小(AP+CP最小值为线段BC的长度).
∵B(5,0),C(0,![]() ),
),
∴直线BC解析式为y=![]() x+
x+![]() ,
,
∵xP=1,∴yP=3,即P(1,3).
(3) (3)存在 设Q(x, ![]() x2+
x2+![]() x+
x+![]() )
)
①若C为直角顶点, 则由△ACO相似于△CQE,得x=5.2
②若A为直角顶点,则由△ACO相似于△AQE,得x=8.2
∴Q的横坐标为5.2 ,7.2
(4)令经过点P(1,3)的直线为y=kx+b,则k+b=3,即b=3-k,
则直线的解析式是:y=kx+3-k,
∵y=kx+3-k,y=![]() x2+
x2+![]() x+
x+![]() ,
,
联立化简得:x2+(4k-2)x-4k-3=0,
∴x1+x2=2-4k,x1x2=-4k-3.
∵y1=kx1+3-k,y2=kx2+3-k,∴y1-y2=k(x1-x2).
根据两点间距离公式得到:![]()
![]()
∴![]() =4(1+k2).
=4(1+k2).
又![]()
![]() ;
;
同理![]()
∴![]()
![]()
![]()
=4(1+k2).
∴M1PM2P=M1M2,
∴![]() 为定值.
为定值.
考点: 二次函数综合题.