��Ŀ����
����Ŀ������С������12�֣�
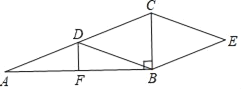
��֪����Rt��ABC��Rt��DEF����ͼ��1���ڷţ���C���E�غϣ�����B��C��E����F��ͬһ��ֱ���ϣ���ACB = ��EDF = 90�㣬��DEF = 45����AC = 8 cm��BC = 6 cm��EF = 9 cm��
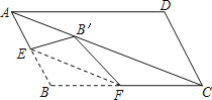
��ͼ��2������DEF��ͼ��1����λ�ó�������1 cm/s���ٶ���CB����ABC��������������DEF������ͬʱ����P����ABC�Ķ���B��������2 cm/s���ٶ���BA���A��������.����DEF�Ķ���D�ƶ���AC����ʱ����DEFֹͣ��������PҲ��ֹ֮ͣ�ƶ���DE��AC�ཻ�ڵ�Q������PQ��������ʱ��Ϊt��s����0��t��4.5����

����������⣺
��1����tΪ��ֵʱ����A���߶�PQ�Ĵ�ֱƽ�����ϣ�
��2������PE�����ı���APEC�����Ϊy��cm2������y��t֮��ĺ�����ϵʽ���Ƿ����ijһʱ��t��ʹ���y��С�������ڣ����y����Сֵ���������ڣ�˵�����ɣ�
��3���Ƿ����ijһʱ��t��ʹP��Q��F������ͬһ��ֱ���ϣ������ڣ������ʱt��ֵ���������ڣ�˵�����ɣ�
���𰸡�
��1��t=2
��2����t = 3ʱ��y��С=![]()
��3����t = 1s����P��Q��F������ͬһ��ֱ����
��������
�⣺��1������A���߶�PQ�Ĵ�ֱƽ�����ϣ�
��AP = AQ.
�ߡ�DEF = 45������ACB = 90�㣬��DEF����ACB����EQC = 180����
���EQC = 45��.
���DEF =��EQC.
��CE = CQ.
������֪��CE = t��BP =2 t��
��CQ = t.
��AQ = 8��t.
��Rt��ABC�У��ɹ��ɶ����ã�AB = 10 cm .
��AP = 10��2 t.
��10��2 t = 8��t.
��ã�t = 2.
�𣺵�t = 2 sʱ����A���߶�PQ�Ĵ�ֱƽ������. 4��
��2����P��![]() ����BE��M����
����BE��M����![]() .
.

��Rt��ABC��Rt��BPM��![]() ��
��
��![]() . ��PM =
. ��PM = ![]() .
.
��BC = 6 cm��CE = t�� �� BE = 6��t.
��y = S��ABC��S��BPE =![]() ��
��![]() =
= ![]() ��
��![]()
=![]() =
= ![]() .
.
��![]() ���������߿�������.
���������߿�������.
����t = 3ʱ��y��С=![]() .
.
�𣺵�t = 3sʱ���ı���APEC�������С����С���Ϊ![]() cm2.8��
cm2.8��
��3����������ijһʱ��t��ʹ��P��Q��F������ͬһ��ֱ����.

��P��![]() ����AC��N��
����AC��N��
��![]() .
.
��![]() �����PAN ����BAC.
�����PAN ����BAC.
��![]() .
.
��![]() .
.
��![]() ��
��![]() .
.
��NQ = AQ��AN��
��NQ = 8��t��(![]() ) =
) = ![]() ��
��
�ߡ�ACB = 90�㣬B��C��E����F��ͬһ��ֱ���ϣ�
���QCF = 90������QCF = ��PNQ.
�ߡ�FQC = ��PQN��
���QCF����QNP .
��![]() . ��
. ��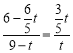 .
.
��![]() ��
��
��ã�t = 1.
�𣺵�t = 1s����P��Q��F������ͬһ��ֱ����. 12��