Question

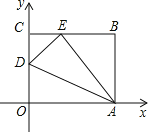
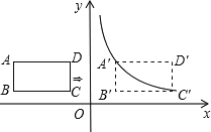
【题目】如图，在平面直角坐标系中，四边形ABCD是矩形，AD∥x轴，A(-3，)，AB=1，AD=2，将矩形ABCD向右平移m个单位，使点A，C恰好同时落在反比例函数y=的图象上，得矩形A′B′C′D′，则反比例函数的解析式为______．

Answer 1

【答案】y=

【解析】

由四边形ABCD是矩形，得到AB=CD=1，BC=AD=2，根据A（-3，），AD∥x轴，即可得到B（-3，），C（-1，），D（-1，）；根据平移的性质将矩形ABCD向右平移m个单位，得到A′（-3+m，），C（-1+m，），由点A′，C′在在反比例函数y=（x＞0）的图象上，得到方程（-3+m）=（-1+m），即可求得结果．

解：∵四边形ABCD是矩形，

∴AB=CD=1，BC=AD=2，

∵A（-3，），AD∥x轴，

∴B（-3，），C（-1，），D（-1，）；

∵将矩形ABCD向右平移m个单位，

∴A′（-3+m，），C（-1+m，），

∵点A′，C′在反比例函数y=（x＞0）的图象上，

∴（-3+m）=（-1+m），

解得：m=4，

∴A′（1，），

∴k=，

∴反比例函数的解析式为：y=．

故答案为y=．