题目内容
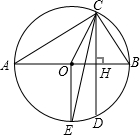
如图所示，在⊙O中，点A在圆内，B、C在圆上，其中OA=7，BC=18，∠A=∠B=60°，则tan∠OBC=______．
过O作OD⊥BC，延长AO，交BC于点E，
∵∠A=∠B=60°，
∴∠OED=60°，∠EOD=30°，
在Rt△ODE中，设DE=x，则OE=2x，OD=
x，
∵OD⊥BC，∴D为BC的中点，即BD=CD=
BC=9，
∵AE=BE，∴7+2x=9+x，
解得：x=2，即OD=2
，
∴tan∠OBC=
=
．
故答案为：
∵∠A=∠B=60°，
∴∠OED=60°，∠EOD=30°，
在Rt△ODE中，设DE=x，则OE=2x，OD=
| 3 |
∵OD⊥BC，∴D为BC的中点，即BD=CD=
| 1 |
| 2 |
∵AE=BE，∴7+2x=9+x，
解得：x=2，即OD=2
| 3 |
∴tan∠OBC=
| OD |
| BD |
2
| ||
| 9 |
故答案为：
2
| ||
| 9 |
练习册系列答案
相关题目
