题目内容
如果两个角的两边两两互相垂直,则这两个角( )
| A、相等 | B、互补 |
| C、相等或互补 | D、不相等也不互补 |
考点:余角和补角
专题:
分析:分类讨论:分一个角再另一角的内部或外部.如图1,∠A与∠B的两边分别垂直,垂足分别为C、D点,则∠ACE=∠BDE=90°,根据三角形内角和定理得到∠A+∠ACD+∠AEC=180°,∠B+∠BDE+∠BED=180°,根据对顶角相等得到∠AEC=∠BED,于是∠A=∠B;如图2,∠A与∠B的两边分别垂直,垂足分别为C、D点,则∠ACE=∠BDE=90°,根据四边形的内角和定理得到∠A+∠ACB+∠B+∠BDA=(4-2)×180°=360°,则∠A+∠B=180°.
解答:解:如图1, ∠A与∠B的两边分别垂直,垂足分别为C、D点,
∠A与∠B的两边分别垂直,垂足分别为C、D点,
则∠ACE=∠BDE=90°,
∵∠A+∠ACD+∠AEC=180°,∠B+∠BDE+∠BED=180°,
而∠AEC=∠BED,
∴∠A=∠B;
如图2,∠A与∠B的两边分别垂直,垂足分别为C、D点,
则∠ACE=∠BDE=90°,
∵∠A+∠ACB+∠B+∠BDA=(4-2)×180°=360°,
∴∠A+∠B=180°.
∴∠A与∠B相等或互补.
故选:C.
 ∠A与∠B的两边分别垂直,垂足分别为C、D点,
∠A与∠B的两边分别垂直,垂足分别为C、D点,则∠ACE=∠BDE=90°,
∵∠A+∠ACD+∠AEC=180°,∠B+∠BDE+∠BED=180°,
而∠AEC=∠BED,
∴∠A=∠B;
如图2,∠A与∠B的两边分别垂直,垂足分别为C、D点,
则∠ACE=∠BDE=90°,
∵∠A+∠ACB+∠B+∠BDA=(4-2)×180°=360°,
∴∠A+∠B=180°.
∴∠A与∠B相等或互补.
故选:C.
点评:本题考查了多边形的内角和定理:n边形的内角和为(n-2)×180°(n≥3).也考查了分类讨论思想的运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列图形:线段、正三角形、平行四边形、矩形、菱形、正方形、等腰梯形、直角梯形,其中既是中心对称图形,又是轴对称图形的共有( )
| A、3个 | B、4个 | C、5个 | D、6个 |
我校一位同学从2015年元月1号开始每天记录当天的最低气温,然后绘成统计图,为了直观反应气温的变化情况,他应选择( )
| A、折线图 | B、扇形图 |
| C、条形图 | D、以上都合适 |
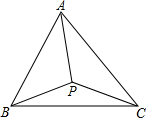 如图,△ABC内有一点P,且PA=PB=PC,若∠PAB=30°,∠PAC=40°,则∠BPC的大小是( )
如图,△ABC内有一点P,且PA=PB=PC,若∠PAB=30°,∠PAC=40°,则∠BPC的大小是( )| A、110° | B、130° |
| C、120° | D、140° |
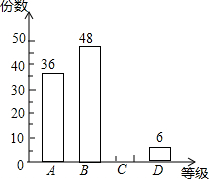 某校为了选拔省教委组织的以“爱我省会•让节能环保称为时尚”为主题的参赛作品,现在本校组织了一次“以爱我家乡•让节能环保成为时尚”的作品征集活动,现从所收集上来的作品中随机爱抽取了一部分,按A,B,C,D四个等级进行评选,并根据评选结果绘制了如图所示的条形统计图,已知等级C的作品的所抽取作品中占25%.
某校为了选拔省教委组织的以“爱我省会•让节能环保称为时尚”为主题的参赛作品,现在本校组织了一次“以爱我家乡•让节能环保成为时尚”的作品征集活动,现从所收集上来的作品中随机爱抽取了一部分,按A,B,C,D四个等级进行评选,并根据评选结果绘制了如图所示的条形统计图,已知等级C的作品的所抽取作品中占25%.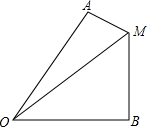 如图,已知∠AOB=60°,MA⊥OA于点A,MB⊥OB于点B,MA=2,MB=11,求OM的长.
如图,已知∠AOB=60°,MA⊥OA于点A,MB⊥OB于点B,MA=2,MB=11,求OM的长. 如图所示,∠A=50°,∠C=80°,∠CBP=∠PBA,∠CDP=∠PDA,求∠P的度数.
如图所示,∠A=50°,∠C=80°,∠CBP=∠PBA,∠CDP=∠PDA,求∠P的度数.