题目内容
9.菱形ABCD的周长为48cm,∠BAD=$\frac{1}{2}$∠ABC,则菱形的面积为72$\sqrt{3}$cm2.分析 连结BD,利用菱形的性质得BC∥AD,则根据平行线的性质得∠DAB+∠ABC=180°,加上∠BAD=$\frac{1}{2}$∠ABC,则可计算出∠DAB=60°,再根据菱形的性质得AB=AD=12,于是可判断△ABD为等边三角形,然后根据等边三角形的面积公式计算出S△ABD=36$\sqrt{3}$,所以S菱形ABCD=2S△ABD=72$\sqrt{3}$(cm2).
解答 解: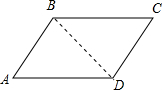 连结BD,如图,
连结BD,如图,
∵四边形ABCD为菱形,
∴BC∥AD,
∴∠DAB+∠ABC=180°,
而∠BAD=$\frac{1}{2}$∠ABC,
∴∠DAB+2∠DAB=180°,
∴∠DAB=60°,
∵菱形ABCD的周长为48,
∴AB=AD=12,
∴△ABD为等边三角形,
∴S△ABD=$\frac{\sqrt{3}}{4}$×122=36$\sqrt{3}$,
∴S菱形ABCD=2S△ABD=72$\sqrt{3}$(cm2).
故答案为72$\sqrt{3}$cm2.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.也考查了等边三角形的判定与性质.

练习册系列答案
相关题目
14.在△ABC中,∠C=90°,BC=6cm,sinA=$\frac{3}{5}$,则AB的长是( )
| A. | 3cm | B. | 4cm | C. | 5cm | D. | 10cm |
1. 如图,直线AB∥CD,一个含60°角的直角三角板EFG(∠E=60°)的直角顶点F在直线AB上,斜边EG与AB相交于点H,CD与FG相交于点M.若∠AHG=50°,则∠FMD等于( )
如图,直线AB∥CD,一个含60°角的直角三角板EFG(∠E=60°)的直角顶点F在直线AB上,斜边EG与AB相交于点H,CD与FG相交于点M.若∠AHG=50°,则∠FMD等于( )
 如图,直线AB∥CD,一个含60°角的直角三角板EFG(∠E=60°)的直角顶点F在直线AB上,斜边EG与AB相交于点H,CD与FG相交于点M.若∠AHG=50°,则∠FMD等于( )
如图,直线AB∥CD,一个含60°角的直角三角板EFG(∠E=60°)的直角顶点F在直线AB上,斜边EG与AB相交于点H,CD与FG相交于点M.若∠AHG=50°,则∠FMD等于( )| A. | 10° | B. | 20° | C. | 30° | D. | 50° |
19.⊙O的半径为5cm,点A到圆心O的距离OA=3cm,则点A与圆O的位置关系为( )
| A. | 点A在圆上 | B. | 点A在圆内 | C. | 点A在圆外 | D. | 无法确定 |
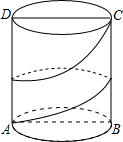 在底面直径为2cm,高为3cm的圆柱体侧面上,用一条无弹性的丝带从A至C按如图所示的圈数缠绕,则丝带的最短长度为3$\sqrt{{π}^{2}+1}$cm.(结果保留π)
在底面直径为2cm,高为3cm的圆柱体侧面上,用一条无弹性的丝带从A至C按如图所示的圈数缠绕,则丝带的最短长度为3$\sqrt{{π}^{2}+1}$cm.(结果保留π)