题目内容
16. 如图,坡上有一颗与水平面EF垂直的大树AB,台风过后,大树倾斜后折断倒在山坡上,大树顶部B接触到坡面上的D点.已知山坡的坡角∠AEF=30°,量得树干倾斜角∠BAC=45°,大树被折断部分和坡面所成的角∠ADC=60°且AD=4米.则这棵大树折断前的高度AB=(2$\sqrt{6}$+2$\sqrt{3}$+2)米.
如图,坡上有一颗与水平面EF垂直的大树AB,台风过后,大树倾斜后折断倒在山坡上,大树顶部B接触到坡面上的D点.已知山坡的坡角∠AEF=30°,量得树干倾斜角∠BAC=45°,大树被折断部分和坡面所成的角∠ADC=60°且AD=4米.则这棵大树折断前的高度AB=(2$\sqrt{6}$+2$\sqrt{3}$+2)米.
分析 过A作AM⊥CD于M,在直角三角形ADM中,求出∠DAM=30°,利用30度角所对的直角边等于斜边的一半求出AM与MD的长,确定出三角形ACM为等腰直角三角形,求出CM,AC的长,由AC+CM+MD求出大树高即可.
解答 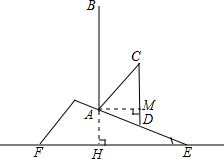 解:过A作AM⊥CD于M,
解:过A作AM⊥CD于M,
则AM=ADsin60°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,MD=$\frac{1}{2}$AD=2.
∵∠C=∠CAM=45°,
∴CM=AM=2$\sqrt{3}$,AC=$\sqrt{2}$AM=2$\sqrt{6}$,
∴AB=AC+CM+MD=2$\sqrt{6}$+2$\sqrt{3}$+2.
∴这棵大树折断前高度为(2$\sqrt{6}$+2$\sqrt{3}$+2)米.
点评 此题属于解直角三角形的应用-坡度坡角问题,涉及的知识有:含30度角的直角三角形的性质,特殊角的三角函数值,等腰直角三角形的性质,熟练掌握性质及定理是解本题的关键.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案
相关题目
7.我们约定:如果身高在166(单位:cm)的±2%范围之内都称为“普通身高”.下面10名男生中的身高(单位:cm)
具有“普通身高”的有几人( )
| 男生序号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | ⑨ | ⑩ |
| 身高x(cm) | 163 | 171 | 173 | 156 | 161 | 174 | 164 | 166 | 169 | 164 |
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
11.在实数-$\frac{2}{5}$、0、-$\sqrt{3}$、2015、π、-$\root{3}{-27}$、0.1$\stackrel{•}{0}$$\stackrel{•}{1}$中,无理数的个数是( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
6.经过某丁字路口的汽车,可能向左转,也可能向右转,如果这两种可能性大小相同,当有三辆汽车经过这个丁字路口时,三辆汽车全部左拐的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{16}$ | D. | $\frac{1}{27}$ |
 的方程
的方程 的解为负数,则m的取值范围是( )
的解为负数,则m的取值范围是( ) B.
B.  C.
C.  D.
D. 
 如图,下列A,B,C,D四个三角形中,能和模板中的△ABC完全重合的是( )
如图,下列A,B,C,D四个三角形中,能和模板中的△ABC完全重合的是( )


