题目内容
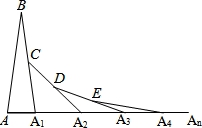
如图,在第1个△ABA1中,∠B=52°,AB=A1B,在A1B上取一点C,延长AA1到A2,使得A1A2=A1C;在A2C上取一点D,延长A1A2到A3,使得A2A3=A2D;…,按此作法进行下去,第2014个三角形的底角的度数为( )
A. B.
B.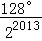 C.
C.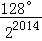 D.
D.
C【考点】等腰三角形的性质.
【专题】规律型.
【分析】先根据等腰三角形的性质求出第1个三角形的底角即∠BA1A的度数,再根据三角形外角的性质及等腰三角形的性质分别求出第2、3、4个三角形的底角即∠CA2A1,∠DA3A2及∠EA4A3的度数,找出规律即可得出第2014个三角形的底角的度数.
【解答】解:∵在△ABA1中,∠B=52°, AB=A1B,
AB=A1B,
∴∠B A1A=
A1A= =
= ,
,
∵A1A2=A1C,∠BA1A是△A1A2C的外角,
∴∠CA2A1= ∠BA1A=
∠BA1A= ;
;
同理可得,∠DA3A2= ,∠EA4A3=
,∠EA4A3= ,
,
∴第2014个三角形的底角的度数为 .
.
故选C.
【点评】本题考查的是等腰三角形的性质及三角形外角的性质,根据题意得出∠CA2A1,∠DA3A2及∠EA4A3的度数,进而找出规律是解答此题的关键.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目





