题目内容
如图,线段AB=1,点P1是线段AB的黄金分割点(AP1<BP1),点P2是线段AP1的黄金分割点(AP2<P1P2),点P3是线段AP2的黄金分割点(AP3<P2P3),…,依此类推,则线段AP2014的长度是 .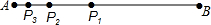
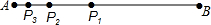
考点:黄金分割
专题:规律型
分析:根据黄金分割的定义得到BP1=
AB,则AP1=AB-
AB=
,则利用同样的方法得到AP2=(
)2,AP3=(
)3,由此可归纳出
线段AP2014的长度.
| ||
| 2 |
| ||
| 2 |
3-
| ||
| 2 |
3-
| ||
| 2 |
3-
| ||
| 2 |
线段AP2014的长度.
解答:解:∵点P1是线段AB的黄金分割点(AP1<BP1),
∴BP1=
AB,
∴AP1=AB-
AB=
AB=
;
∵点P2是线段AP1的黄金分割点(AP2<P1P2),
∴AP2=
AP1=(
)2,
同理可得AP3=(
)3,
∴AP2014=(
)2014.
故答案为(
)2014.
∴BP1=
| ||
| 2 |
∴AP1=AB-
| ||
| 2 |
3-
| ||
| 2 |
3-
| ||
| 2 |
∵点P2是线段AP1的黄金分割点(AP2<P1P2),
∴AP2=
3-
| ||
| 2 |
3-
| ||
| 2 |
同理可得AP3=(
3-
| ||
| 2 |
∴AP2014=(
3-
| ||
| 2 |
故答案为(
3-
| ||
| 2 |
点评:本题考查了黄金分割:把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即AB:AC=AC:BC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点.其中AC=
AB≈0.618AB,并且线段AB的黄金分割点有两个.
| ||
| 2 |

练习册系列答案
相关题目
 在△ABC和△ADE中,AC=AB,AE=AD,∠CAB=∠EAD=90°.
在△ABC和△ADE中,AC=AB,AE=AD,∠CAB=∠EAD=90°.