题目内容
10.某景点的门票价格规定如表:| 购票人数 | 1-50人 | 51-100人 | 100人以上 |
| 每人门票价 | 13元 | 11元 | 8元 |
(2)你认为有没有最省购票费用的方案?若有,请写出你的方案,并按照你的方案计算一下能省多少钱?
分析 设(1)班x人,(2)班y人,根据两班共104人及两班都以班为单位分别购票,则一共应付1240元可得出方程组,解出即可得出答案
解答 解:(1)设(1)班x人,(2)班y人,
则x+y=104,13x+11y=1240,
解得x=48,y=56.
(2)两班联合作为一个团体购票8×104=832元,
节省1240-832=408元.
最省购票费用的方案:两班合在一起购票,可省408元.
点评 此题是一元二次方程组的应用,考查了列二元一次方程组解实际问题的运用,二元一次方程组的解法的运用,解答时建立方程组求出各班的人数是关键.

练习册系列答案
相关题目
18.点P(-3,2)在平面直角坐标系中所在的象限是( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
15.甲、乙两种商品原来的单价和为100元.因市场变化,甲商品降价10%,乙商品提价40%,调价后,两种商品的单价之和比原来的单价之和提高了20%.若设甲、乙商品原来的单价分别为x元、y元,则下面根据题意,所列方程组正确的是( )
| A. | $\left\{\begin{array}{l}{x+y=100}\\{(1+10%)x+(1-40%)y=100×(1+20%)}\end{array}\right.$ | |
| B. | $\left\{\begin{array}{l}{x+y=100}\\{(1-10%)x+(1+40%)y=100×(1+20%)}\end{array}\right.$ | |
| C. | $\left\{\begin{array}{l}{x+y=100}\\{(1-10%)x+(1+40%)y=100×20%}\end{array}\right.$ | |
| D. | $\left\{\begin{array}{l}{x+y=100}\\{(1+10%)x+(1-40%)y=100×20%}\end{array}\right.$ |
2. 如图,已知∠1=∠2,则下列结论正确的是( )
如图,已知∠1=∠2,则下列结论正确的是( )
 如图,已知∠1=∠2,则下列结论正确的是( )
如图,已知∠1=∠2,则下列结论正确的是( )| A. | c∥d | B. | a∥b | C. | ∠3=∠1 | D. | ∠2=∠4 |
19.在平面直角坐标系内,若点M(x+2,x-1)在第四象限.那么x的取值范围是( )
| A. | x>-2 | B. | x<-2 | C. | -2<x<1 | D. | x>1 |
 已知数据总数是30,在样本频数分布直方图(如图)中,各小长方形的高之比为AE:BF:CG:DH=2:4:3:1,第二小组的频数为12.
已知数据总数是30,在样本频数分布直方图(如图)中,各小长方形的高之比为AE:BF:CG:DH=2:4:3:1,第二小组的频数为12.
 如图的正方形地板,是由9块除颜色外完全相同的正方形地砖拼接而成的,其中黑色地砖5块,一个小球在这块地板上自由滚动,并随机地停在某块方砖上,它停留在黑色方砖上的概率为$\frac{5}{9}$.
如图的正方形地板,是由9块除颜色外完全相同的正方形地砖拼接而成的,其中黑色地砖5块,一个小球在这块地板上自由滚动,并随机地停在某块方砖上,它停留在黑色方砖上的概率为$\frac{5}{9}$.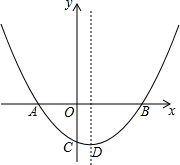 如图,抛物线y=ax2+bx-1(a≠0)经过A(-1,0),B(2,0)两点,与y轴交于点C.
如图,抛物线y=ax2+bx-1(a≠0)经过A(-1,0),B(2,0)两点,与y轴交于点C.