题目内容
7.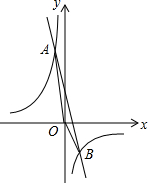 如图,已知反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b的图象交于A(-1,10),B(2,n)两点.
如图,已知反比例函数y=$\frac{{k}_{1}}{x}$与一次函数y=k2x+b的图象交于A(-1,10),B(2,n)两点.(1)求k1,k2,b的值;
(2)求△AOB的面积;
(3)根据函数图象,写出一次函数值大于反比例函数值的自变量x的取值范围.
分析 (1)由点A的坐标,利用待定系数法即可求出k1的值,由点B的横坐标利用反比例函数图象上点的坐标特征可得出点B的坐标,再根据点A、B的坐标利用待定系数法即可求出k2、b的值;
(2)设直线y=-5x+5与x轴交于点C,利用一次函数图象上点的坐标特征求出点C的坐标,利用三角形的面积公式结合S△AOB=S△AOC+S△BOC,即可得出△AOB的面积;
(3)根据两函数图象的上下位置关系,即可得出一次函数值大于反比例函数值的自变量x的取值范围.
解答 解:(1)∵反比例函数y=$\frac{{k}_{1}}{x}$过点A(-1,10),
∴k1=-10,
∵点B(2,n)在反比例函数y=-$\frac{10}{x}$的图象上,
∴n=-$\frac{10}{2}$=-5.
将A(-1,10)、B(2,-5)代入y=k2x+b,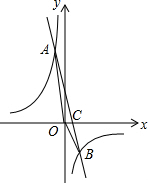
得$\left\{\begin{array}{l}{-{k}_{2}+b=10}\\{2{k}_{2}+b=-5}\end{array}\right.$,解得:$\left\{\begin{array}{l}{{k}_{2}=-5}\\{b=5}\end{array}\right.$.
∴k1=-10,k2=-5,b=5.
(2)设直线y=-5x+5与x轴交于点C,
当y=-5x+5=0,x=1,
∴OC=1,
∴S△AOB=S△AOC+S△BOC=$\frac{1}{2}$×1×10+$\frac{1}{2}$×1×5=$\frac{15}{2}$.
(3)观察函数图象,可知:当x<-1或0<x<2时,一次函数图象在反比例函数图象上方,
∴一次函数值大于反比例函数值的自变量x的取值范围为x<-1或0<x<2.
点评 本题考查了反比例函数与一次函数的交点问题、待定系数法求反比例(一次)函数解析式、反比例(一次)函数图象上点的坐标特征以及三角形的面积,解题的关键是:(1)根据点的坐标,利用待定系数法求出反比例(一次)函数解析式;(2)利用分割图形法求三角形的面积;(3)根据两函数图象的上下位置关系,找出结论.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| 摸球次数 | 40 | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 360 | 400 |
| 出现红色的频数 | 14 | 24 | 38 | 68 | 77 | 92 | 109 | 120 | 132 | |
| 出球红色的频率 | 35% | 32% | 35% | 34% | 33% | 34% |
(2)画出摸出红球频率的折线统计图;
(3)摸出一个红球的概率估计值是多少?
 如图,圆柱体的高为4cm,底面周长为6cm,小蚂蚁在圆柱表面爬行,从A点到B点,路线如图所示,则最短路程为5cm.
如图,圆柱体的高为4cm,底面周长为6cm,小蚂蚁在圆柱表面爬行,从A点到B点,路线如图所示,则最短路程为5cm.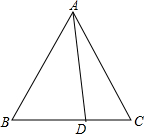 如图,在等边△ABC中,点D为BC边上一点,请你用量角器,在AC边上确定点E,使AE=CD,简述你的作法,并说明理由.
如图,在等边△ABC中,点D为BC边上一点,请你用量角器,在AC边上确定点E,使AE=CD,简述你的作法,并说明理由.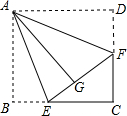 如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°.
如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°. 将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起.
将一副三角板中的两块直角三角尺的直角顶点C按如图所示的方式叠放在一起.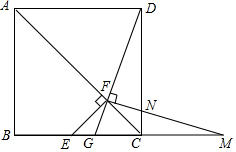 如图.在正方形ABCD中,点E是BC边上的中点,EF⊥AC于点F.连接DF并延长交BC于G.过F作FM⊥DG交CD于N,交BC的延长线于点M.
如图.在正方形ABCD中,点E是BC边上的中点,EF⊥AC于点F.连接DF并延长交BC于G.过F作FM⊥DG交CD于N,交BC的延长线于点M. 如图所示,AB⊥l1,AC⊥l2,则点A到直线l1的距离是线段AB的长度.
如图所示,AB⊥l1,AC⊥l2,则点A到直线l1的距离是线段AB的长度.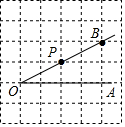 点P是∠AOB的边OB上一点.
点P是∠AOB的边OB上一点.